Nov 9, 2022 | Volume 12 - Issue 3
Michael T. Kalkbrenner, Gabriella Miceli
Meeting the mental health needs of students enrolled in science, technology, engineering, and mathematics (STEM) majors is particularly challenging for professional counselors who work in college settings, as STEM students are a subgroup of college students that face unique risks for developing mental health issues. The scarcity of literature on STEM student mental health coupled with their reticence to seek counseling is concerning. An important next step in this line of research is understanding why STEM students are reticent to seek counseling. Accordingly, the present investigators validated STEM students’ scores on the Revised Fit, Stigma, and Value (RFSV) Scale, a screening tool for measuring barriers to seeking counseling. Results also established the capacity of STEM students’ RFSV scores to predict peer-to-peer referrals to the counseling center and revealed demographic differences in barriers to counseling. Findings have implications for enhancing professional counselors’ efforts to support STEM students’ mental health.
Keywords: Revised Fit, Stigma, and Value Scale; STEM; student mental health; barriers to counseling; peer-to-peer referrals
The frequency and complexity of college students presenting with mental health issues is a notable concern for professional counselors who work in university settings (Al-Maraira & Shennaq, 2021; Hong et al., 2022). Students enrolled in science, technology, engineering, and mathematics (STEM) majors are a distinctive group of college students who face unique risks for developing mental health issues (Daker et al., 2021; Kalkbrenner, James, & Pérez-Rojas, 2022; Lipson et al., 2016; Shapiro & Sax, 2011). When compared to their non-STEM counterparts, STEM students are less likely to recognize warning signs of mental distress, and they access mental health support services at lower rates than their peers. In addition, the harsh and competitive academic environment in STEM majors can exacerbate students’ risk for mental health distress (Lipson et al., 2016; Shapiro & Sax, 2011). Moreover, Rice et al. (2015) demonstrated that STEM students exhibit higher levels of maladaptive perfectionism, which is associated with higher levels of mental distress.
Whereas substantial academic and financial resources exist to support STEM students (U.S. Department of Education, 2020), there is a dearth of literature on supporting STEM students’ mental health, which is essential for retaining students and ensuring their success both in and out of the classroom (Kivlighan et al., 2021; Schwitzer et al., 2018). This gap in the literature is concerning, as STEM students are at risk for mental health issues, which can lead to attrition, isolation, and suicide (Daker et al., 2021; Kalkbrenner, James, & Pérez-Rojas, 2022; Lipson et al., 2016). As just one example, academic mental health distress is a significant predictor of lower enrollment and completion rates in STEM fields (Daker et al., 2021). Moreover, Muenks et al. (2020) found that higher levels of psychological vulnerability among STEM students was a significant predictor of lower class attendance, higher dropout intentions, and less class engagement.
The literature is lacking research on why STEM students tend to seek counseling at lower rates than non-STEM students. One of the first steps in supporting STEM students’ mental health is validating scores on a screening tool for identifying barriers to accessing mental health support services among STEM students. Although screening tools that appraise barriers to counseling exist, none of them have been validated with STEM students. The Revised Fit, Stigma, and Value (RFSV) Scale is a screening tool for appraising barriers to counseling that has been normed with non–college-based populations (e.g., adults in the United States; Kalkbrenner & Neukrug, 2018) and college students with mental health backgrounds (e.g., graduate counseling students; Kalkbrenner & Neukrug, 2019), as just a few examples. When compared to the existing normative RFSV Scale samples, STEM students are a distinct college student population who utilize counseling services at lower rates than students in mental health majors (e.g., psychology; Kalkbrenner, James, & Pérez-Rojas, 2022). The psychometric properties of instrumentation can fluctuate significantly between different populations, and researchers and practitioners have an ethical obligation to validate scores on instruments before interpreting the results with untested populations (Mvududu & Sink, 2013). Accordingly, the primary aims of the present study were to validate STEM students’ scores on the RFSV Scale (Kalkbrenner & Neukrug, 2019), test the capacity of RFSV scores for predicting referrals to the counseling center, and investigate demographic differences in STEM students’ RFSV scores.
The Revised Fit, Stigma, and Value (RFSV) Scale
Neukrug et al. (2017) developed and validated scores on the original version of the Fit, Stigma, and Value (FSV) Scale for appraising barriers to counseling among a large sample of human services professionals. The FSV Scale contains the three following subscales or latent traits behind why one would be reluctant to seek personal counseling: Fit, Stigma, and Value. Kalkbrenner et al. (2019) validated scores on a more concise version of the FSV Scale, which became known as the RFSV Scale, which includes the same three subscales as the original version. Building on this line of research, Kalkbrenner and Neukrug (2019) found a higher-order factor, the Global Barriers to Counseling scale. The Global Barriers to Counseling scale is composed of a total composite score across the three single-order subscales (Fit, Stigma, and Value). Accordingly, the Fit, Stigma, and Value subscales can be scored separately and/or users can compute a total score for the higher-order Global Barriers to Counseling scale.
Scores on the RFSV Scale have been validated with a number of non-college populations, including adults in the United States (Kalkbrenner & Neukrug, 2018), professional counselors (Kalkbrenner et al., 2019), counselors-in-training (Kalkbrenner & Neukrug, 2019), and high school students (Kalkbrenner, Goodman-Scott, & Neukrug, 2020). If scores are validated with STEM students, the RFSV Scale could be used to enhance professional counselors’ mental health screening efforts to understand and promote STEM student mental health. Specifically, campus-wide mental health screening has implications for promoting peer-to-peer mental health support. For example, college counselors are implementing peer-to-peer mental health support initiatives by training students to recognize warning signs of mental distress in their peers and, in some instances, refer them to college counseling services (Kalkbrenner, Sink, & Smith, 2020).
Peer-to-Peer Mental Health Support
College students tend to discuss mental health concerns with their peers more often than with a faculty member or student affairs professional (Wawrzynski et al., 2011; Woodhead et al., 2021). To this end, the popularity and utility of peer-to-peer mental health support initiatives has grown in recent years (Kalkbrenner, Lopez, & Gibbs, 2020; Olson et al., 2016). The effectiveness of these peer-to-peer support initiatives can be evaluated by test scores (e.g., scores on mental distress and well-being inventories) as well as non-test criteria (e.g., increases in the frequency of peer-to-peer mental health referrals). For example, Olson et al. (2016) found that college students who attended a Recognize & Refer workshop were significantly more likely to refer a peer to counseling when compared to students who did not attend the workshop. Similarly, Kalkbrenner, Lopez, and Gibbs (2020) found that increases in college students’ awareness of warning signs for mental distress were predictive of substantial increases in the odds of making peer-to-peer referrals to the counseling center.
Peer-to-peer mental health support also has implications for improving college student mental health (Bryan & Arkowitz, 2015; Byrom, 2018; Caporale-Berkowitz, 2022). For example, Bryan and Arkowitz (2015) found that peer-run support programs for depression were associated with significant reductions in depressive symptoms. In addition, Byrom (2018) demonstrated that peer support interventions were associated with increases in college students’ well-being. The synthesized results of the studies cited in this section suggest that peer-to-peer mental health support has utility for promoting mental health among general samples of undergraduate college students. However, to the best of our knowledge, the literature is lacking research on peer-to-peer mental health support with STEM majors, a subgroup of college students with unique mental health needs (Daker et al., 2021; Lipson et al., 2016; Shapiro & Sax, 2011).
The Present Study
College counseling services are a valuable resource for students, as attendance in counseling is associated with increases in GPA and retention rates (Kivlighan et al., 2021; Lockard et al., 2019; Schwitzer et al., 2018). Considering STEM students’ unique vulnerability to mental health distress (Daker et al., 2021; Lipson et al., 2016; Shapiro & Sax, 2011) and their reticence to seek counseling (Kalkbrenner, James, & Pérez-Rojas, 2022), professional counselors who work in university settings need screening tools with validated scores for identifying why STEM students might avoid accessing counseling services. The RFSV Scale has potential to fill this gap in the measurement literature, as a number of recent psychometric studies (e.g., Kalkbrenner, Goodman-Scott, & Neukrug, 2020; Kalkbrenner & Neukrug, 2018) demonstrated support for the psychometric properties of scores on the RFSV Scale with non-college populations. However, the literature is lacking a screening tool for appraising barriers to counseling with validated scores among STEM students. Accordingly, a score validation study with STEM students is an important next step in this line of research, as the internal structure of instrumentation can vary notably between different samples (Mvududu & Sink, 2013). The literature is also lacking research on the potential of peer-to-peer mental support (e.g., students recognizing and referring a peer to counseling) among STEM students. This is another notable gap in the literature, as college students are more likely to discuss mental health concerns with a peer than with faculty or other university personnel (Wawrzynski et al., 2011; Woodhead et al., 2021). If STEM students’ scores on the RFSV Scale are validated, we will proceed to test the capacity of scores for predicting peer-to-peer referrals to the counseling center as well as examine demographic differences in STEM students’ RFSV scores.
The findings of the present investigation have implications for campus-wide mental health screening, increasing peer-to-peer mental health support, and identifying subgroups of STEM students that might be particularly reticent to seek counseling. To this end, the following research questions (RQs) and hypotheses (Ha) guided the present investigation: RQ1: Is the internal structure of scores on the RFSV Scale confirmed with STEM students? Ha1: The dimensionality of the RFSV Scale will be confirmed with STEM students. RQ2: Are STEM students’ RFSV scores significant predictors of making at least one referral to the counseling center? Ha2: Higher RFSV scores will emerge as a statistically significant positive predictor of STEM students making one or more peer referrals to the counseling center. RQ3: Are there significant demographic differences in FSV barriers to counseling among STEM students? Ha3: Statistically significant demographic differences in STEM students’ RFSV scores will emerge.
Methods
Participants and Procedures
Following IRB approval, first author Michael T. Kalkbrenner obtained an email list from the Office of University Student Records of all students who were enrolled in a STEM major at a research-intensive university with four campus locations in three cities located in the Southwestern United States. A recruitment message was sent out to the email list via Qualtrics Secure Online Survey Platform. A total of 407 prospective participants clicked on the survey link. A response rate could not be calculated, as Qualtrics does not track inaccurate or inactive email addresses. A review of the raw data revealed 41 cases with 100% missing data. Likely, these 41 prospective participants clicked on the link to the survey and decided not to participate. Following the removal of those 41 cases, less than 20% of data were missing for the remaining 366 cases. Little’s Missing Completely at Random test indicated that the data could be treated as missing completely at random (p = .118) and expectation maximization was used to impute missing values. An investigation of standardized z-scores revealed six univariate outliers (z > ± 3.29) and Mahalanobis distances displayed eight multivariate outliers, which were removed from the data set, yielding a robust sample of N = 352.
Participants ranged in age from 18 to 63 (M = 24.29; SD = 8.59). The demographic profile for gender identity consisted of 65.1% (n = 229) female, 30.4% (n = 107) male, 2.0% (n = 7) non-binary, 1.1% (n = 4) transgender, 0.6% (n = 2) an identity not listed (“please specify”), and 0.9% (n = 3) prefer not to answer. The ethnoracial demographic profile consisted of 2.6% (n = 9) Native Indian or Alaska Native; 3.1% (n = 11) Asian or Asian American; 2.0% (n = 7) Black or African American; 48.3% (n = 170) Hispanic, Latinx, or Spanish origin; 2.0% (n = 7) Middle Eastern or North African; 3.4% (n = 12) Multiethnic; 36.6% (n = 129) White or European American; 1.1% (n = 4) Another race, ethnicity, or origin (“please specify”); and 0.9% (n = 3) preferred not to answer. The present sample was composed of notably more diverse groups of STEM students when compared to national estimates of STEM students (National Center for Educational Statistics [NCES], 2020). The NCES’s estimates revealed fewer women (33.0%, n = 263,034) and Latinx (12.3%, n = 94,927) STEM students as well as fewer White students (49.8%, n = 385,132). But the NCES’s national estimates included larger proportions of Black (7.2%, n = 55,642) and Asian (11.0%, n = 85,135) STEM students when compared to the present sample.
Instrumentation
Participants completed a demographic questionnaire by indicating their informed consent, then confirming they met the following inclusion criteria for participation: (a) 18 years or older, (b) enrolled in at least one undergraduate STEM course, and (c) currently a STEM major. The demographic questionnaire concluded with questions about respondents’ age, gender identity, ethnoracial identity, help-seeking history, and if they had referred one or more peers to the counseling center.
The Revised FSV Scale
The RFSV Scale is a screening tool that was designed to measure barriers to seeking counseling (Kalkbrenner, Neukrug, & Griffith, 2019). Participants respond to a prompt (“I am less likely to attend counseling because . . . ”) for 14 declarative statements on the following Likert scale: 1 = Strongly Disagree, 2 = Disagree, 3 = Neither Agree nor Disagree, 4 = Agree, or 5 = Strongly Agree. The RFSV Scale is composed of three subscales or latent traits behind one’s reticence to seek counseling, including Fit, Stigma, and Value. Scores on the Fit subscale can range from 5 to 25, with higher scores indicating more restraint from seeking counseling because one believes the process of counseling is not suitable with their personal worldview (e.g., “I couldn’t find a counselor who would understand me”). Scores on the Stigma subscale also range from 5 to 25, and higher scores denote a greater hesitation to seek counseling due to feelings of embarrassment or shame (e.g., “It would damage my reputation”). Scores on the Value subscale range from 4 to 20, with higher scores indicating a greater disinclination to seek counseling because they believe the effort required would not be worth the potential benefits (e.g., “Counseling is unnecessary because my problems will resolve naturally”).
The Global Barriers to Counseling scale is composed of test takers’ average composite score across the three Fit, Stigma, and Value subscales and produces an overall estimation of a test taker’s sensitivity to barriers toward seeking counseling. Scores on the Global Barriers to Counseling scale range from 13 to 65, with higher scores indicating a greater reticence to seek counseling. The collective findings of past investigators demonstrated evidence for the internal structure validity (confirmatory factor analysis) and internal consistency reliability (α = .70 to α = .91) of scores on the RFSV Scale with a number of non-college populations (Kalkbrenner, Goodman-Scott, & Neukrug, 2020; Kalkbrenner & Neukrug, 2018, 2019; Kalkbrenner et al., 2019).
Data Analysis
A confirmatory factor analysis (CFA) based on structural equation modeling was computed in IBM SPSS AMOS version 26 to answer the first RQ about the dimensionality of STEM students’ RFSV scores. We used the joint suggestions from Dimitrov (2012) and Schreiber et al. (2006) for acceptable model fit in CFA: chi-square absolute fit index (CMIN; non-significant p-value or χ2 to df < 3), comparative fit index (CFI; .90 to .95 = acceptable fit and > .95 = close fit), root mean square error of approximation (RMSEA; ≤ .08), and the standardized root mean square residual (SRMR; ≤ .08). Internal consistency reliability evidence of test scores is another important step in testing a scale’s psychometric properties. Cronbach’s coefficient alpha (α) is the most popular internal consistency reliability estimate; however, its proper use is dependent on the data meeting several statistical assumptions (McNeish, 2018). Composite internal consistency reliability estimates, such as McDonald’s coefficient omega (ω), tend to produce more stable reliability estimates of scores. Accordingly, the present investigators computed both α and ω.
College students are more likely to discuss mental health concerns with their peers than with faculty, staff, or other university personnel (Wawrzynski et al., 2011; Woodhead et al., 2021). Accordingly, college counseling researchers and practitioners are devoting more time to peer-to-peer mental health support initiatives with the goal of increasing peer-to-peer referrals to the counseling center (Kalkbrenner, Sink, & Smith, 2020; Olson et al., 2016). Past investigators (e.g., Kalkbrenner, Neukrug, & Esquivel, 2022) found that the RFSV barriers were significant predictors of peer-to-peer referrals to the counseling center with non-STEM students. To test the generalizability of this finding with STEM students, we conducted a logistic regression analysis to answer the second RQ regarding the capacity of STEM students’ RFSV scores to predict at least one peer referral to the counseling center. STEM students’ interval-level composite scores on the Fit, Stigma, and Value subscales were entered into the model as predictor variables. The criterion variable was quantified on a categorical scale. On the demographic questionnaire, students responded to the following question: “Have you ever referred (recommended) another student to counseling services?” and selected either “0 = never referred a peer to the counseling center” or “1 = referred one or more peers to the counseling center.”
A 2(gender) X 3(race/ethnicity) X 2(help-seeking history) multivariate analysis of variance (MANOVA) was computed to investigate the third RQ regarding demographic differences in RFSV barriers among STEM students. The three categorical-level independent variables included gender (male or female), race/ethnicity (Latinx, White, or other ethnicity), and help-seeking history (never attended counseling or attended at least one counseling session). The three interval-level dependent variables included STEM students’ composite scores on the Fit, Stigma, and Value subscales. Discriminant analysis was employed as a post hoc test for MANOVA (Warne, 2014).
Results
The RFSV Scale items were entered into a CFA to test the dimensionality of scores with STEM students (RQ1). Excluding the CMIN (χ2 [74] = 257.55, p < .001, χ2 to df = 3.48), results revealed a satisfactory model fit: CFI = .92; RMSEA = .08, 90% CI [.07, .10]; and SRMR = .08. The CMIN tends to underestimate model fit with samples that are large enough for CFA (Dimitrov, 2012). Thus, adequate internal structure validity evidence of scores was achieved based on the collective CFI, RMSEA, and SRMR results. The standardized factor loadings were all acceptable-to-strong and ranged from .48 to .90 (see Figure 1, Model 1).
Figure 1
Revised FSV Scale Path Models With Standardized Coefficients
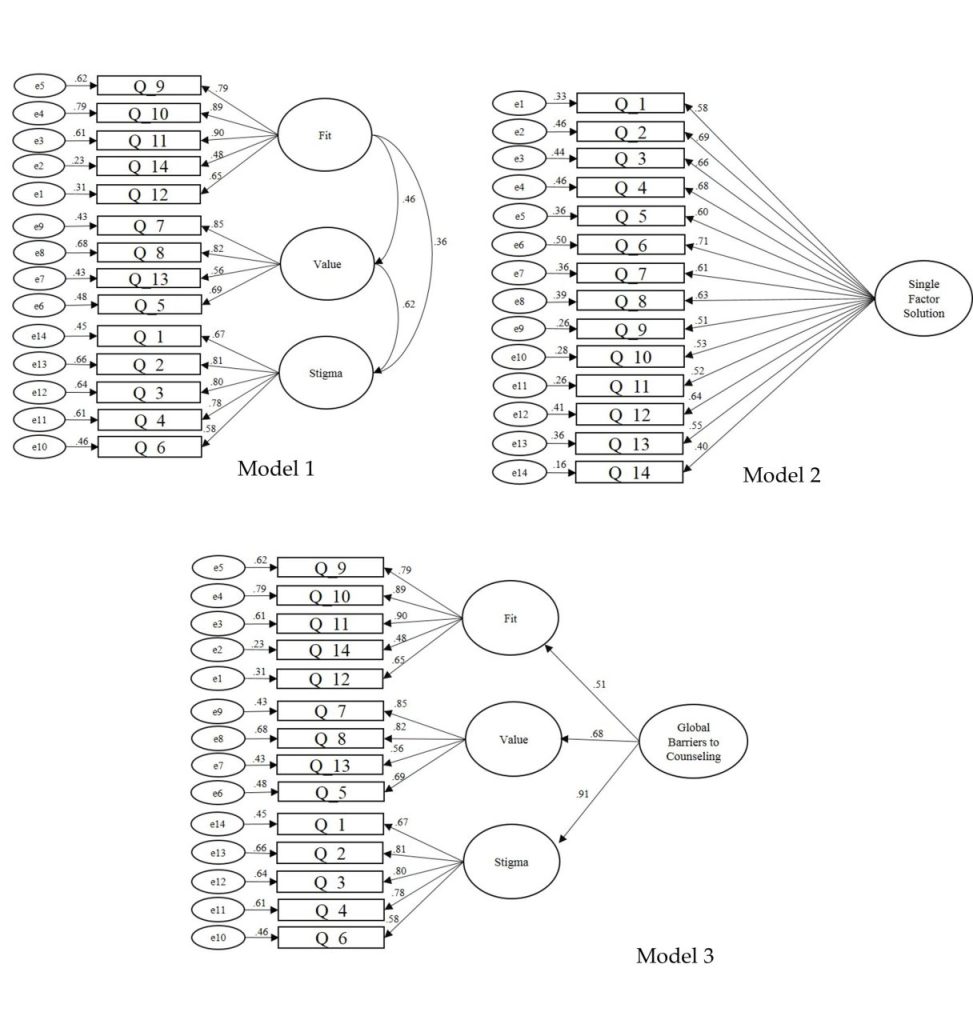
Based on the findings of Kalkbrenner and Neukrug (2019), we computed a higher-order confirmatory factor analysis (HCFA) to test for a Global Barriers to Counseling scale. As expected, the single-factor RFSV model (see Figure 1, Model 2) revealed poor model fit: CMIN (χ2 [77] = 1,013.71, p < .001, χ2 to df = 13.17); CFI = .61; RMSEA = .19, 90% CI [.18, .20]; and SRMR = .13. Accordingly, the theoretical support for a higher-order model (Kalkbrenner & Neukrug, 2019) coupled with the poor fitting single-factor model (see Figure 1, Model 2) indicated that computing an HCFA was appropriate. Except for the CMIN (χ2 [74] = 257.55, p < .001, χ2 to df = 3.48), the higher-order model (see Figure 1, Model 3) displayed a satisfactory model fit: CFI = .92; RMSEA = .08, 90% CI [.07, .10]; and SRMR = .08. Tests of internal consistency reliability revealed satisfactory reliability evidence of scores on the Fit (α = .84, ω = .83), Stigma (α = .86, ω = .87), and Value (α = .79, ω = .79) subscales and the Global Barriers to Counseling scale (α = .88, ω = .88).
STEM students’ RFSV scores were entered into a logistic regression analysis to answer RQ2 regarding the capacity of STEM students’ RFSV scores to predict at least one referral to the counseling center. The logistic regression model was statistically significant, X2(1) = 80.97, p < .001, Nagelkerke R2 = .064. The odds ratios, Exp(B), revealed that a decrease of one unit in STEM students’ scores on the Value subscale (higher scores = less value toward counseling) was associated with a decrease in the odds of having made at least one peer-to-peer referral to the counseling center by a factor of .559.
A factorial MANOVA was computed to answer RQ3 regarding demographic differences in RFSV barriers among STEM students. A significant main effect emerged for gender on the combined dependent variables, F(3, 316) = 5.23, p = .002, Pillai’s Trace = 0.05, η2p = 0.047. The post hoc discriminant analysis (DA) revealed a significant discriminant function, Wilks λ = 0.93, χ2 = 23.60, df = 3, canonical correlation = 0.26, p < .001. The standardized canonical discriminant function coefficients between the latent factors and discriminant functions showed that the Value factor loaded more strongly on the discriminant function (1.10) than the Stigma (0.17) or Fit (−0.62) factors. The mean discriminant score on the function for male participants was 0.40. The mean discriminant score on the function for female participants was −0.19. In other words, the MANOVA and post hoc DA revealed that male STEM students scored significantly higher (higher scores reflect greater reluctance to seek counseling) on the Value barrier when compared to female STEM students.
A significant main effect also emerged for help-seeking history on the combined dependent variables, F(3, 467) = 4.65, p = .003, Pillai’s Trace = 0.04, η2p = 0.042. The post hoc DA displayed a significant discriminant function, Wilks λ = 0.93, χ2 = 24.10, df = 3, canonical correlation = 0.26, p < .001. The standardized canonical discriminant function coefficients between the latent factors and discriminant functions showed that the Value factor loaded more strongly on the discriminant function (1.10) than the Stigma (0.01) or Fit (−0.71) factors. The mean discriminant score on the function for participants without a help-seeking history was 0.25. The mean discriminant score on the function for participants with a help-seeking history was −0.29. In other words, the MANOVA and post hoc DA showed that STEM students without a help-seeking history scored significantly higher on the Value barrier than STEM students with a help-seeking history.
Discussion
The purpose of the present study was to validate STEM students’ scores on the RFSV Scale and investigate demographic correlates with the Fit, Stigma, and Value barriers. The CFA results demonstrated that the RFSV Scale and its dimensions were estimated adequately with a sample of STEM students. This finding is consistent with the existing body of literature on the generalizability of scores on the RFSV Scale with a number of non-college populations (e.g., Kalkbrenner, Goodman-Scott, & Neukrug, 2020; Kalkbrenner & Neukrug, 2018). In addition to a stringent test of internal structure validity, CFA is also a theory-testing procedure (Mvududu & Sink, 2013). Thus, our CFA results indicated that Fit, Stigma, and Value comprise a tri-dimensional theoretical model of barriers to counseling among STEM students. Consistent with the results of Kalkbrenner and Neukrug (2019), we found support for a higher-order Global Barriers to Counseling scale. The presence of a higher-order factor (see Figure 1, Model 3) indicates that the covariation between the first-order Fit, Stigma, and Value subscales comprises a meta-level latent trait. Collectively, the single-order and higher-order CFA results indicate that Fit, Stigma, and Value are discrete dimensions of an interconnected latent trait. Accordingly, CFA results provided support for the dimensionality of both the single-order RFSV model (see Figure 1, Model 1) and the higher-order model (see Figure 1, Model 3) with STEM students.
STEM students face unique risks for mental health issues, including maladaptive perfectionism as well as intense pressure to perform in harsh and competitive academic environments (Rice et al. 2015; Shapiro & Sax, 2011). These unique risk factors coupled with STEM students’ reticence to seek counseling (Kalkbrenner, James, & Pérez-Rojas, 2022) created a need for a screening tool for appraising why STEM students might avoid accessing counseling services. The results of the CFA and HCFA in the present study begin to address the gap in the literature regarding the lack of a screening tool with validated scores for appraising barriers to counseling among STEM students. Our CFA and HCFA results suggest that college counselors can use the RFSV Scale as one way to understand why STEM students on their campus are reluctant to access counseling services.
Consistent with the findings of Kalkbrenner and Neukrug (2019), we found statistically significant differences in peer-to-peer referrals and demographic differences in STEM students’ scores on the Value barrier. Specifically, increases in STEM students’ belief in the value of attending counseling were associated with significant increases in the odds of making one or more peer referrals to the counseling center, as indicated by the moderate effect size of the finding. It appears that STEM students’ attendance in personal counseling increases their propensity for recommending counseling to their peers. Similar to Kalkbrenner and Neukrug (2018), tests of group demographic differences revealed that STEM students in the present study with a help-seeking history were less sensitive to the Value barrier than STEM students without a help-seeking history. These findings indicate that attendance in counseling might enhance STEM students’ belief that the effort required to attend counseling is worth the benefits. Perhaps experiencing counseling firsthand increases STEM students’ belief in the value of counseling as well as their disposition to refer a peer to counseling. This finding has particularly important implications, as STEM students are a distinct college-based population with unique mental health needs who tend to utilize mental health support services at lower rates than non-STEM students (Kalkbrenner, James, & Pérez-Rojas, 2022; Rice et al., 2015; Shapiro & Sax, 2011). In particular, our results suggest that STEM students who access counseling services usually see value in the process. STEM students’ general attitudes about counseling might become more positive if more and more STEM students participate in counseling.
Also, consistent with the findings of Kalkbrenner and Neukrug (2018), we found demographic differences in STEM students’ scores on the Value barrier by gender identity, with males attributing less value to attending counseling than females. Macro- and micro-systemic gender role forces tend to contribute to men’s reticence to seek counseling (Neukrug et al., 2013). These forces might be intensified among male STEM students considering the intersectionality between gender roles and the high-pressure environment in STEM majors to not show vulnerability (Lipson et al., 2016; Neukrug et al., 2013). Specifically, gender-role pressures to avoid showing vulnerability coupled with a high-pressure academic environment might make male STEM students especially reluctant to seek counseling. Men are also less likely than women to recognize and seek treatment for mental health issues (Kalkbrenner & Neukrug 2018; Neukrug et al., 2013). Thus, it is also possible that male STEM students are less likely to recognize mental distress as a potentially serious health issue, which contributes to them placing less value on the benefits of counseling when compared to their female counterparts. Future research is needed to test these possible explanations for this finding.
Implications
The findings of this study have a number of implications for professional counselors who work in college settings. The CFA and HCFA results extend the psychometric properties of the RFSV Scale to STEM students (RQ1), which is an important contribution to the measurement literature, as the scale offers professional counselors a brief screening tool that usually takes 10 minutes or less to complete. The RFSV Scale can be administered at the systemic level (e.g., all STEM students at a university). Tests of internal structure reveal support for a three-dimensional RFSV model (see Figure 1, Model 1) as well as a higher-order model (see Figure 1, Model 3) with STEM students. Accordingly, professional counselors can administer and score one or both RFSV models depending on their mental health screening goals. The Global Barriers to Counseling scale might have utility for college counselors who are aiming to gather baseline information about STEM students’ general reticence to seek counseling. The three-dimensional model can provide more specific information (Fit, Stigma, and/or Value) about the reasons why STEM students on a particular campus are reluctant to seek counseling.
Our results reveal that increases in STEM students’ scores on the Value subscale were associated with a noteworthy increase in the odds of making a peer-to-peer referral to the counseling center. This finding coupled with STEM students’ vulnerability to mental distress (Daker et al., 2021; Kalkbrenner, James, & Pérez-Rojas, 2022; Lipson et al., 2016; Shapiro & Sax, 2011) suggests that peer-to-peer referrals to mental health support services might be more important than ever before in connecting STEM students in mental distress to support services. Professional counselors who work in college settings can administer the RFSV Scale to STEM students and use the results as one method of informing the content of peer-to-peer mental health support initiatives. If, for example, STEM students on a particular campus score higher on the Value subscale (higher scores denote less value toward counseling), there might be utility in including information about the many benefits of counseling in peer-to-peer outreach initiatives for STEM students. Specifically, it might be beneficial to discuss both the academic and personal benefits associated with attending counseling. For groups of STEM students who score higher on the Stigma scale, college counselors might take a strengths-based perspective by discussing how attending counseling takes courage and strength.
College counselors and student affairs officials can reach STEM students by partnering with STEM faculty and administrators to attend STEM orientations and classes that are held in large lecture halls. College counselors may build relationships with department heads and program directors of STEM programs through sharing empirical evidence on STEM students’ unique mental health needs and their reticence to access mental health support services (Kalkbrenner, James, & Pérez-Rojas, 2022; Lipson et al., 2016; Shapiro & Sax, 2011). College counselors might also discuss how increases in STEM students’ mental health is associated with greater retention and academic success, which are key values in STEM programs (Daker et al., 2021; Lockard et al., 2019; Meaders et al., 2020; Muenks et al., 2020). As buy-in from STEM department heads and program directors increases, there might be utility in professional counselors regularly making presentations and facilitating discussions about mental health and the benefits of attending counseling during new STEM student orientations. The content of these presentations can be based on the extant literature regarding the socio-personal factors that can place STEM students at risk for mental distress—for example, maladaptive perfectionism (Rice et al., 2015), high-pressure academic environments (Shapiro & Sax, 2011), and difficulty recognizing warning signs for mental distress (Kalkbrenner, James, & Pérez-Rojas, 2022). Once STEM students learn about these socio-personal factors, the presentation content can shift to psychoeducation about the utility of counseling for improving both personal and academic outcomes (Lockard et al., 2019).
The RFSV Scale can also be administered on more targeted levels, for example, to specific groups of STEM students who might be particularly vulnerable to mental health distress. There might be utility in administering the RFSV Scale to male STEM students considering that we found male STEM students were more sensitive to the Value barrier than female STEM students. College counselors can use the RFSV results to identify specific barriers (e.g., Value) that might be making STEM students on their campus unlikely to access counseling services. Such results can be used to inform thes curriculum of mental health programming (e.g., peer-to-peer support initiatives). When working with male STEM students, college counselors might consider the intersectionality of academic pressure (Lipson et al., 2016) and gender-role–based mental health stressors (Neukrug et al., 2013) they might be facing. In all likelihood, considering the intersectionality between these socio-personal factors will help college counselors address their clients’ presenting concerns holistically.
Limitations and Future Research
The methodological limitations of this research should be reviewed when considering the implications of the results. The preset data were collected from STEM students in three different cities located in the Southwestern United States; however, results might not generalize to STEM students in other geographical locations. Future researchers can validate RFSV scores with national and international samples of STEM students. Moreover, the findings of cross-sectional research designs are correlational, which prevents researchers from drawing conclusions regarding cause-and-effect. Now that STEM students’ scores on the RFSV Scale are validated, future investigators can extend this line of inquiry by conducting outcome research on the effectiveness of interventions geared toward promoting the utilization of mental health support services among STEM students.
Although factor analytic results in the present study were promising, STEM students are not a homogenous group. To this end, future investigators can extend this line of research by conducting factorial invariance testing to examine the psychometric equivalence of RFSV scores across subgroups of STEM students. As just one example, past investigators (e.g., Shapiro & Sax, 2011) found differences in STEM students’ mental health by gender identity. Relatedly, our results did not reveal demographic differences by race/ethnicity in STEM students’ vulnerability to barriers to counseling. However, we used a dummy-coding procedure to create racial/ethnic identity comparison groups (Latinx, White, or other ethnicity) that were large enough for statistical analyses. Clustering participants with racial/ethnic identities other than White or Latinx into one group might have masked significant findings within the other race/ethnicity group. It is also possible that some participants identified as White and Latinx, as White is a racial category and Latinx is an ethnic category. Future researchers should examine potential disparities in barriers to counseling among more racially and ethnically diverse samples of STEM students. In an extension of the extant literature on samples of primarily male STEM students, the present study included notably more (> 50%) female STEM students when compared to a national demographic profile of STEM students (NCES, 2020). However, the findings of the present study might not generalize to STEM students with gender identities that extend beyond only male or female. Accordingly, future researchers can test the invariance of RFSV scores with more gender-diverse samples.
The findings of the CFA and HCFA in the present study supported Fit, Stigma, and Value as barriers to counseling among STEM students. However, the deductive nature of quantitative research does not capture the nuances of participants’ lived experiences. One way that future investigators can extend this line of research is through qualitative investigations of STEM students’ attitudes and values about seeking counseling services. Qualitative results might reveal important nuances and insights into STEM students’ propensity to access mental health support services.
Conclusion
To the best of our knowledge, the present investigation is the first to establish the psychometric properties of a barriers to counseling tool with STEM students. The results represent an important contribution to the measurement literature, as confirming the internal structure of test scores on an existing measure with a previously untested population is a vital step in demonstrating construct validity. We also found that decreases in STEM students’ reticence to seek counseling was predictive of statistically significant increases in the odds of making a peer referral to the counseling center. In addition, results revealed demographic differences in barriers to counseling among STEM students by gender and help-seeking history. Collectively, our findings suggest that professional counselors who work in college settings can use the RFSV Scale as one way to support STEM college student mental health by identifying why STEM students might be reticent to access counseling services. Supporting STEM students’ mental health has implications for increasing their retention rates, completion rates, and overall psychological well-being.
Conflict of Interest and Funding Disclosure
The authors reported no conflict of interest
or funding contributions for the development
of this manuscript.
References
Al-Maraira, O. A., & Shennaq, S. Z. (2021). Investigation of depression, anxiety and stress levels of health-care students during COVID-19 pandemic. Mental Health Review Journal, 26(2), 113–127.
https://doi.org/10.1108/MHRJ-10-2020-0070
Bryan, A. E. B., & Arkowitz, H. (2015). Meta-analysis of the effects of peer-administered psychosocial interventions on symptoms of depression. American Journal of Community Psychology, 55(3–4), 455–471. https://doi.org/10.1007/s10464-015-9718-y
Byrom, N. (2018). An evaluation of a peer support intervention for student mental health. Journal of Mental Health, 27(3), 240–246. https://doi.org/10.1080/09638237.2018.1437605
Caporale-Berkowitz, N. A. (2022). Let’s teach peer support skills to all college students: Here’s how and why. Journal of American College Health, 70(7), 1921–1925. https://doi.org/10.1080/07448481.2020.1841775
Daker, R. J., Gattas, S. U., Sokolowski, H. M., Green, A. E., & Lyons, I. M. (2021). First-year students’ math anxiety predicts STEM avoidance and underperformance throughout university, independently of math ability. NPJ Science of Learning, 6(1), Article 17. https://doi.org/10.1038/s41539-021-00095-7
Dimitrov, D. M. (2012). Statistical methods for validation of assessment scale data in counseling and related fields. American Counseling Association.
Hong, V., Busby, D. R., O’Chel, S., & King, C. A. (2022). University students presenting for psychiatric emergency services: Socio-demographic and clinical factors related to service utilization and suicide risk. Journal of American College Health, 70(3), 773–782. https://doi.org/10.1080/07448481.2020.1764004
Kalkbrenner, M. T., Goodman-Scott, E., & Neukrug, E. S. (2020). Validation of high school students’ scores on the Revised Fit, Stigma, and Value Scale: Implications for school counseling screening. Professional School Counseling, 23(1). https://doi.org/10.1177/2156759X20912750
Kalkbrenner, M. T., James, C., & Pérez-Rojas, A. E. (2022). College students’ awareness of mental disorders and resources: Comparison across academic disciplines. Journal of College Student Psychotherapy, 36(2), 113–134. https://doi.org/10.1080/87568225.2020.1791774
Kalkbrenner, M. T., Lopez, A. L., & Gibbs, J. R. (2020). Establishing the initial validity of the REDFLAGS Model: Implications for college counselors. Journal of College Counseling, 23(2), 98–112. https://doi.org/10.1002/jocc.12152
Kalkbrenner, M. T., & Neukrug, E. S. (2018). Identifying barriers to attendance in counseling among adults in the United States: Confirming the factor structure of the Revised Fit, Stigma, & Value Scale. The Professional Counselor, 8(4), 299–313. https://doi.org/10.15241/mtk.8.4.299
Kalkbrenner, M. T., & Neukrug, E. S. (2019). The utility of the Revised Fit, Stigma, and Value Scale with counselor trainees: Implications for enhancing clinical supervision. The Clinical Supervisor, 38(2), 262–280. https://doi.org/10.1080/07325223.2019.1634665
Kalkbrenner, M. T., Neukrug, E. S., & Esquivel, L. E. (2022). Mental health literacy screening of students in Hispanic Serving Institutions. Journal of Counseling & Development, 100(3), 319–329. https://doi.org/10.1002/jcad.12428
Kalkbrenner, M. T., Neukrug, E. S., & Griffith, S. A. (2019). Appraising counselor attendance in counseling: The validation and application of the Revised Fit, Stigma, and Value Scale. Journal of Mental Health Counseling, 41(1), 21–35. https://doi.org/10.17744/mehc.41.1.03
Kalkbrenner, M. T., Sink, C. A., & Smith, J. L. (2020). Mental health literacy and peer-to-peer counseling referrals among community college students. Journal of Counseling & Development, 98(2), 172–182. https://doi.org/10.1002/jcad.12311
Kivlighan, D. M., III, Schreier, B. A., Gates, C., Hong, J. E., Corkery, J. M., Anderson, C. L., & Keeton, P. M. (2021). The role of mental health counseling in college students’ academic success: An interrupted time series analysis. Journal of Counseling Psychology, 68(5), 562–570. https://doi.org/10.1037/cou0000534
Lipson, S. K., Zhou, S., Wagner, B., Beck, K., & Eisenberg, D. (2016). Major differences: Variations in undergraduate and graduate student mental health and treatment utilization across academic disciplines. Journal of College Student Psychotherapy, 30(1), 23–41. https://doi.org/10.1080/87568225.2016.1105657
Lockard, A. J., Hayes, J. A., Locke, B. D., Bieschke, K. J., & Castonguay, L. G. (2019). Helping those who help themselves: Does counseling enhance retention? Journal of Counseling & Development, 97(2), 128–139. https://doi.org/10.1002/jcad.12244
McNeish, D. (2018). Thanks coefficient alpha, we’ll take it from here. Psychological Methods, 23(3), 412–433. https://doi.org/10.1037/met0000144
Meaders, C. L., Lane, A. K., Morozov, A. I., Shuman, J. K., Toth, E. S., Stains, M., Stetzer, M. R., Vinson, E., Couch, B. A., & Smith, M. K. (2020). Undergraduate student concerns in introductory STEM courses: What they are, how they change, and what influences them. Journal for STEM Education Research, 3(2), 195–216. https://doi.org/10.1007/s41979-020-00031-1
Muenks, K., Canning, E. A., LaCosse, J., Green, D. J., Zirkel, S., Garcia, J. A., & Murphy, M. C. (2020). Does my professor think my ability can change? Students’ perceptions of their STEM professors’ mindset beliefs predict their psychological vulnerability, engagement, and performance in class. Journal of Experimental Psychology, 149(11), 2119–2144. https://doi.org/10.1037/xge0000763
Mvududu, N. H., & Sink, C. A. (2013). Factor analysis in counseling research and practice. Counseling Outcome Research and Evaluation, 4(2), 75–98. https://doi.org/10.1177/2150137813494766
National Center for Educational Statistics. (2020). Science, Technology, Engineering, and Mathematics (STEM) education, by gender. https://nces.ed.gov/fastfacts/display.asp?id=899
Neukrug, E., Britton, B. S., & Crews, R. C. (2013). Common health-related concerns of men: Implications for counselors. Journal of Counseling & Development, 91(4), 390–397. https://doi.org/10.1002/j.1556-6676.2013.00109
Neukrug, E. S., Kalkbrenner, M. T., & Griffith, S.-A. M. (2017). Barriers to counseling among human service professionals: The development and validation of the Fit, Stigma, & Value (FSV) Scale. Journal of Human Services, 37(1), 27–40. https://digitalcommons.odu.edu/cgi/viewcontent.cgi?article=1016&context=chs_pubs
Olson, K., Koscak, G., Foroudi, P., Mitalas, E., & Noble, L. (2016). Recognize and refer: Engaging the Greek community in active bystander training. College Student Affairs Journal, 34(3), 48–61. https://doi.org/10.1353/csj.2016.0018
Rice, K. G., Ray, M. E., Davis, D. E., DeBlaere, C., & Ashby, J. S. (2015). Perfectionism and longitudinal patterns of stress for STEM majors: Implications for academic performance. Journal of Counseling Psychology, 62(4), 718–731. https://doi.org/10.1037/cou0000097
Rincon, B. E., & George-Jackson, C. E. (2016). STEM intervention programs: Funding practices and challenges. Studies in Higher Education, 41(3), 429–444. https://doi.org/10.1080/03075079.2014.927845
Schreiber, J. B., Nora, A., Stage, F. K., Barlow, E. A., & King, J. (2006). Reporting structural equation modeling and confirmatory factor analysis results: A review. The Journal of Educational Research, 99(6), 323–338. https://doi.org/10.3200/JOER.99.6.323-338
Schwitzer, A. M., Moss, C. B., Pribesh, S. L., St. John, D. J., Burnett, D. D., Thompson, L. H., & Foss, J. J. (2018). Students with mental health needs: College counseling experiences and academic success. Journal of College Student Development, 59(1), 3–20. https://doi.org/10.1353/csd.2018.0001
Shapiro, C. A., & Sax, L. J. (2011). Major selection and persistence for women in STEM. New Directions for Institutional Research, 2011(152), 5–18. https://doi.org/10.1002/ir.404
U.S. Department of Education. (2020). Science, technology, engineering, and math, including computer science. https://www.ed.gov/stem
Warne, R. (2014). A primer on multivariate analysis of variance (MANOVA) for behavioral scientists. Practical Assessment, Research, and Evaluation, 19, 1–10. https://doi.org/10.7275/sm63-7h70
Wawrzynski, M. R., LoConte, C. L., & Straker, E. J. (2011). Learning outcomes for peer educators: The national survey on peer education. Emerging Issues and Practices in Peer Education, 2011(133), 17–27.
https://doi.org/10.1002/ss.381
Woodhead, E. L., Chin-Newman, C., Spink, K., Hoang, M., & Smith, S. A. (2021). College students’ disclosure of mental health problems on campus. Journal of American College Health, 69(7), 734–741.
https://doi.org/10.1080/07448481.2019.170653
Michael T. Kalkbrenner, PhD, NCC, is an associate professor at New Mexico State University. Gabriella Miceli, MS, LPC-A, is a doctoral student at New Mexico State University. Correspondence may be addressed to Michael T. Kalkbrenner, 1780 E. University Ave., Las Cruces, NM 88003, mkalk001@nmsu.edu.
Nov 9, 2021 | Volume 11 - Issue 4
Dana L. Brookover
Access to school counseling services leads to access to college-readiness counseling initiatives, including science, technology, engineering, and mathematics (STEM) education–focused counseling for students. School counselor caseload and percentage of time spent on college-readiness counseling were analyzed in relation to longitudinal STEM postsecondary outcomes of students in a nationally representative sample. Access to school counselors who spend 21% or more of their time on college-readiness counseling predicted persistence and attainment of a STEM postsecondary degree. The current results offer implications for school counselors, counselor educators, and future researchers, including the need for STEM self-efficacy interventions, unbiased curriculum, and professional development on STEM counseling for school counselors; and the call for a more nuanced understanding of this topic.
Keywords: STEM, school counseling, college-readiness counseling, longitudinal, self-efficacy
College and career readiness are key outcome targets of school systems across the United States (Malin et al., 2017; U.S. Department of Education, 2010). Science, technology, engineering, and mathematics (STEM) initiatives are also a national priority (The White House, Office of Science and Technology Policy, National Science and Technology Council, 2018). School counselors play an integral role in their students’ college readiness through providing college-readiness counseling (Gilfillan, 2017). This includes the important role school counselors perform in educating students on the possibilities in STEM at the college level (Cabell et al., 2021; Schmidt et al., 2012).
STEM Education
STEM education has been described by Tsupros and colleagues (2009) as an interdisciplinary approach to learning science, technology, engineering, and mathematics that includes understanding and knowledge of science and math concepts, computers, and problem-solving skills. There have been long-standing calls for a more STEM-literate workforce, a more diverse STEM workforce, and more individuals interested in working in the STEM fields in general (Mohr-Schroeder et al., 2015).
STEM education attainment and persistence is an emerging topic in the career development and counseling profession, but there are differing opinions on what constitutes the “STEM crisis” (Xue & Larson, 2015). Some researchers have indicated that the demand for STEM workers in the United States will not be met because of a lack of qualified and interested individuals to step into these positions. Another viewpoint emphasizes that research has indicated there are both shortages and surpluses of STEM workers, depending on the particular job market segment (Xue & Larson, 2015). Still, the data is clear that there is a “STEM crisis” in terms of inequities in who is matriculating into and persisting in STEM majors (National Science Foundation [NSF], 2021).
Despite the great growth in traditionally underrepresented students persisting in STEM majors in college (NSF, 2021) and the potential for career development initiatives to increase retention in STEM for minority groups (Belser et al., 2018), there are still disparities in STEM college major attainment and persistence by gender, race and ethnicity, socioeconomic status (SES), and first-generation college student (FGCS) status (Chen, 2013). This is an equity issue, as the choice to enroll in a STEM postsecondary program may also lead to higher pay and the potential for positive job marketability given the projected growth in available positions (Cataldi et al., 2014; Vilorio, 2014). Hence, school counselors are called upon to address STEM education disparities in their work, as the American School Counselor Association (ASCA; 2019) emphasizes the role of the school counselor in working to ensure equitable postsecondary opportunities and outcomes for all students.
College-Readiness Counseling and STEM Education
High school counselors are in a unique position to provide career-readiness counseling, including college-readiness counseling for those students who aim to attend college after high school. College-readiness counseling involves developmentally appropriate counseling that engages students in (a) creating postsecondary goals and expectations, (b) building an awareness of interests and abilities, and (c) receiving information and support for their college access and success (Savitz-Romer, 2012). School counselors can focus on STEM education with students in each of these tasks.
Research has shown that students’ intent to pursue a STEM career already varies by populations as early as the ninth grade. Girls and students in minority racial groups, in a nationally representative sample, were less likely to expect to work in a STEM discipline at the age of 30 as compared to boys and White students (Mau & Li, 2018). Students’ SES also predicted STEM career aspirations, in that a student with higher SES was more likely to aspire to a STEM career (Mau & Li, 2018). There are multiple potential reasons for the opportunity gaps in STEM higher education, including lack of engagement in higher-level STEM coursework in high school, the time it takes to complete STEM programs, and a student’s lack of financial ability to do so, as well as attitudinal factors, such as motivation and confidence. These factors can lead to less matriculation into a STEM major and more attrition (Chen, 2013). There may also be a lack of support and encouragement and even direct discouragement from educators for underrepresented minorities and women to engage in STEM coursework, starting in adolescence (Grossman & Porche, 2014). This was echoed in a qualitative study in which high school counselors said that a barrier in their work supporting underrepresented students in STEM was a lack of anti-racist curricula in STEM classes and inconsistencies in anti-racist practice by teachers (Cabell et al., 2021). The importance of college-readiness counseling focused on STEM education is known.
Existing STEM Education–Focused College-Readiness Counseling Research
Emerging research is developing on the school counselor’s role on students’ STEM self-efficacy and students’ pursuit of postsecondary STEM education (Cabell et al., 2021; Falco, 2017; Falco & Summers, 2019; Schmidt et al., 2012). Falco (2017) provided a conceptual framework with the goal of helping school counselors better support STEM career development for all students and especially those from underrepresented groups. Falco suggested school counselors can encourage students to take advanced-level math and science courses, provide classroom instruction on the benefits of engaging in STEM, ensure balanced gender and racial/ethnic ratios in STEM classes, and organize a peer mentoring program or conduct small group counseling on relevant skills.
Cabell and colleagues (2021) interviewed high school counselors about their work with underrepresented students and STEM education. The participants were actively engaging in college-readiness counseling focused on STEM education with students, but there were barriers to their ability to support underrepresented students’ STEM interests, including lack of time, in part from administrative tasks, and large caseloads (Cabell et al., 2021). This is related to previous research suggesting that the percentage of time spent on college-readiness counseling differs by school characteristics. For example, private school counselors typically spend more time on it than public school counselors, and school counselors with more students on free-and-reduced lunch tend to spend less time (Clinedinst & Koranteng, 2017). Smaller caseloads have also been associated with school counselors spending more than half their time on college-readiness counseling (Engberg & Gilbert, 2014). Further, smaller caseloads show improved college outcomes, including higher rates of 4-year college enrollment (Engberg & Gilbert, 2014; Hurwitz & Howell, 2014).
Schmidt and colleagues (2012) also provided suggestions for school counselors to “expand their repertoire” through STEM-focused career development. Key impact areas include academic and career counseling, and leadership and advocacy. The researchers acknowledged how school climate and the large administrative demands (i.e., duties inappropriate for counselors) placed on school counselors may restrict their ability to engage in career-related and STEM course discussions with students. However, there is no data to shed light on the long-term impacts of this barrier and how their suggested key impact areas influence student outcomes.
Research has found that self-efficacy is an important pathway to students’ STEM major persistence (Lent et al., 2016; Rittmayer & Beier, 2009). Self-efficacy is an individual’s belief in their ability to influence and control the events of their life to obtain desired performances (Bandura, 1994). As an example, when students believe they can achieve desired results in science through their abilities and actions, this is considered high science self-efficacy. Researchers have detailed the results of a career group intervention that incorporated the sources of self-efficacy and addressed perceived career barriers with the goals of improving the career decision self-efficacy and STEM self-efficacy for adolescent girls (Falco & Summers, 2019). Components of the intervention included a group counseling structure, career psychoeducation, journaling, constructing a timeline of successful previous performances, progressive muscle relaxation, vicarious learning, and verbal persuasion by the leader. Results showed significantly different improvements in career decision self-efficacy and STEM self-efficacy. The results of this intervention are promising, especially as it is one of the few empirical studies on self-efficacy counseling interventions and STEM career outcomes with adolescents. The sample was all female with half of the sample identifying as Latina (Falco & Summers, 2019).
It follows that there needs to be access to school counseling services for engagement in college counseling that can effectively bolster students’ STEM aspirations. Given the potential for high school STEM interventions to make a great impact in student’s STEM self-efficacy and education outcomes, the inability of school counselors to provide college counseling, and specifically STEM-focused college counseling, is troubling (Falco & Summers, 2019). To move forward in advocating for school counseling access to promote student outcomes in the STEM pipeline, a theory-driven, longitudinal approach to investigating the impact of school counseling access on this outcome was initiated in the current study. Given the importance of considering student characteristics, environmental inputs, and self-efficacy in STEM matriculation, attainment, and persistence, social cognitive career theory (Lent et al., 1994) served as a logical base for the theoretical framework for this investigation.
Social Cognitive Career Theory
Social cognitive career theory (SCCT) was developed from Albert Bandura’s (1986) social cognitive theory to create a unifying theory of career and academic interest, choice, and performance (Lent et al., 1994). SCCT accounts for the cyclical nature of making a career choice through accounting for people receiving information from contextual influences that fuel feedback loops (Lent, 2004). These external influences can be contextual supports or barriers (Lent et al., 2000). It is also important to note that one’s perception of barriers moderates the relationship between interests and career choices (Brown & Lent, 1996). Hence, underrepresented and underserved students’ perceptions of barriers in obtaining a STEM degree can impact career choice and development. Moreover, other background environmental influences, person inputs, and behaviors interact in this feedback loop as well. One influence of utmost importance in the theory is self-efficacy. Thus, SCCT can account for external factors, otherwise known as proximal environmental influences (e.g., school counseling access), and individual characteristics (e.g., demographics and self-efficacy) within long-term career development formation.
Purpose of the Study
The current study was built upon previous SCCT school counseling and STEM attainment and persistence studies. The goal was to investigate the long-term impacts of school counseling access, in relation to student characteristics, on STEM outcomes. The research question guiding the study was: Do school counselor caseload and percentage of time spent on college-readiness counseling predict STEM major attainment and persistence?
Method
Using a multivariate, quantitative, longitudinal research design to answer the research question was well-suited to the purpose of the study. Longitudinal research designs allow for gathering and analyzing data on development over time (Lavrakas, 2008). As the research question was focused on prediction in a sample of students and the outcome was measured quantitatively, this research design was employed. I followed the process of secondary analysis of existing data (Cheng & Phillips, 2014), utilizing the High School Longitudinal Study of 2009 (HSLS:09), developed by the National Center for Education Statistics (NCES; 2020a). The HSLS:09 dataset followed a sample of high school students throughout their secondary education career into postsecondary years (NCES, 2020b).
Participants and Sampling
The HSLS:09 is a longitudinal study of over 23,000 ninth graders from 944 schools (Ingels & Dalton, 2013; NCES, 2020b). Stratified random sampling ensured a nationally representative sample. Approximately 900 high school counselors were surveyed for the study to provide information on their school counseling departments, including school counselor caseload and percentage of time spent on college-readiness counseling. School counselors in the study were not randomly selected; rather, they were either the lead counselor or the counselor deemed most knowledgeable about the ninth graders at the time of the baseline data collection (Ingels & Dalton, 2013). The baseline data was collected in 2009, then the study had a first follow-up survey with student participants in 2012; there was a brief 2013 update survey and a second follow-up in 2016 (Duprey et al., 2018).
Data Selection
Cheng and Phillips’s (2014) steps for secondary analysis of existing data under the research question–driven approach guided the data collection procedures for the current study. Thus, I determined which variables in the existing dataset to use to answer the research question. This was done through using SCCT to guide the model creation. Then, I became acquainted with the coding patterns of variables. This led to the transformation of distributions of select variables to meet assumptions of the model to be used in analysis when necessary, as detailed below.
Constructs and Variables
The HSLS:09 variables (NCES, 2020a) included in the current study both cover the research question and fit within the theoretical framework (i.e., SCCT; Lent et al., 1994). First, there are demographic variables, also known as person inputs and background environmental influences, within SCCT. Data on variables to represent self-efficacy constructs were also selected. Two variables measured school counselor caseload and school counselor percentage of time spent on college-readiness counseling. Finally, the outcome variable was STEM major attainment and persistence.
First-Generation College Student Status
The FGCS status variable was constructed as a variable detailing the highest level of education achieved by either parent/guardian in the sample member’s home in the HSLS:09 dataset. This was created from two composite variables within the dataset: highest education level of Parent 1 and highest education level of Parent 2. In its original categorical form, there are seven categories for parent highest level of education, but for the current study, it was recoded into a dichotomous/dummy variable; either the student had a parent in the home who has a bachelor’s degree or a more advanced degree, or the student did not have a parent in the home who has a bachelor’s or a more advanced degree.
Race/Ethnicity
Race/ethnicity information was provided through dichotomous race/ethnicity composites based on data from the student questionnaire, if available. If not available from the student questionnaire, they were based on, in order of preference: data from the school-provided sampling roster or data from the parent questionnaire. The designations included in the HSLS:09 and the current study are: (a) American Indian or Alaskan Native; (b) Asian; (c) Black (African American); (d) Hispanic, no race specified; (e) Hispanic, race specified; (f) more than one race; (g) Native Hawaiian/Pacific Islander; and (h) White. For the current study, the two Hispanic categories were combined.
Sex
This variable was categorical and referred to the sex of the sample member (male or female) and was provided by the student if possible, and if not, the parent or school roster. The labels male and female have held and continue to hold “powerful associations” (Lips, 2020, p. 3), and not all people identify into a gender binary of female and male (Lips, 2020). There is a gender variable assessed in the HSLS:09 study; however, it is only available in the restricted use dataset, so the sex variable was utilized in the current study.
Socioeconomic Status
SES was a composite variable consisting of five components obtained from the parent/guardian questionnaire and aligned with previous NCES longitudinal study methods for calculating SES: (a) the highest education among parents/guardians in the two-parent family of a responding student, or the education of the sole parent/guardian; (b) the education level of the other parent/guardian in the two-parent family; (c) the highest occupational prestige score among parents/guardians in the two-parent family of a responding student, or the prestige score of the sole parent/guardian; (d) the occupation prestige score of the other parent/guardian in the two-parent family; and (e) family income. This was a standardized value set to 0; hence, values ranged from −1.82 to 2.57.
Self-Efficacy Variables
This data was collected at the baseline. SCCT asserts that learning experiences and prior accomplishments are an integral part of forming self-efficacy; hence STEM grade point average (GPA) was included under self-efficacy (Lent et al., 1994). GPA information was collected at the 2013 update.
Math Self-Efficacy. Math self-efficacy is a continuous variable, with higher values representing higher math self-efficacy. The information was assessed through a scale consisting of four items (e.g., “can do excellent job on math tests”). The variable was created through principal components factor analysis and was standardized to a mean of 0 and standard deviation of 1. Only respondents who provided a full set of responses were assigned a scale value. The coefficient of reliability (demonstrated by alpha) for the scale is .65 (NCES, 2020c).
Science Self-Efficacy. Science self-efficacy is also a continuous variable, with higher values representing higher science self-efficacy, and was also created through principal components factor analysis and standardized to a mean of 0 and standard deviation of 1. There were four items on the scale (e.g., “can master skills in science course”). Only respondents who provided a full set of responses were assigned a scale value. The coefficient of reliability (indicated by alpha) for the scale is .65 (NCES, 2020c).
STEM GPA
STEM GPA, an interval variable, was computed during the 2013 update through high school transcript composites. STEM GPA values range from 0.25 to 4, in increments of 0.25.
School Counselor Caseload
Information for this continuous variable was assessed through one item on the school counselor questionnaire: “On average, what is the caseload for a counselor in this school? Students per counselor.” Students per counselor ranged from 2 to 999 (NCES, 2020c). The variable was recoded into a dichotomous variable, with 0 indicating a school counselor caseload of 250 or less, and 1 indicating a school counselor caseload of 251 or more. The ASCA-recommended caseload number for school counselors is 250:1.
School Counselor Percentage of Time Spent on College-Readiness Counseling
This was assessed through one item on the school counselor questionnaire that read, “Last school year (2008–2009), what percentage of work hours did your school’s counseling staff spend assisting students with college readiness, selection, and applications?” Responses were reported according to the following categories: 5% or less, 6%–10%, 11%–20%, 21%–50%, and more than 50%. This was recoded to a dichotomous variable—20% or less time spent on college-readiness counseling or 21% or more time spent on college-readiness counseling—reflecting a cut-off of the national average of time spent on college-readiness counseling by school counselors at 21% (Clinedinst & Koranteng, 2017).
Outcome Variable: STEM Major Attainment and Persistence
This was a dichotomous variable (either Not STEM or STEM) and was collected in the second follow-up study in 2016 (i.e., approximately 3 years post–high school graduation). It referred to how the respondent declared or decided upon their degree and whether that undergraduate degree or certificate is in a STEM field of study.
Data Analysis
Continuing to follow Cheng and Phillips’s (2014) steps for secondary analysis of existing data, the first step in data analysis was to run preliminary analyses of descriptive statistics and bivariate correlations. Then, I assessed missing data patterns. When deemed necessary, the HSLS:09 developers did utilize imputation of values (Ingels & Dalton, 2013). Imputation allows the use of all study respondent records in an analysis, affording more power for statistical tests. Additionally, if the imputation procedure is effective, then the analysis results can be less biased than if there were missing data unaccounted for (Ingels & Dalton, 2013). Value imputation occurred in place of missing responses for select variables identified from the student and parent questionnaires through single-value imputation (Duprey et al., 2018; Ingels & Dalton, 2013). Further, the NCES provides analytic weighted variables and replication weights associated with those main sampling weights. The analytic weights make estimates from the sample data representative of the target population (i.e., ninth grade students in 2009–2010). These analytic weights account not only for differential selection probabilities, but also for differential patterns of response and nonresponse—in other words, nonresponse bias (Duprey et al., 2018). In addition to the analytic weight variables accounting for stratified sampling and nonresponse bias, replication weight variables address standard error concerns. Standard error calculation ensures appropriate standard errors based on the differences between the estimates of the full sample and a series of replicates (Duprey et al., 2018). These replication weights are done with the balanced repeated replication method and help account for the possibility of artificially low standard errors due to clustering in sampling (Duprey et al., 2018).
Prior to running the sequential logistic regression, assumptions testing was completed. Logistic regression analyses allow the use of criterion measures on a binary outcome (Meyers et al., 2017). The result of a logistic regression is the impact of each variable on the probability of the observed event of interest (Sperandei, 2014). Sequential logistic regression allows the researcher to specify the entry order of predictor variables into the model (Tabachnick & Fidell, 2013).
Model 1, the baseline model, represented person inputs and background environmental influences in SCCT. It included the following variables: FGCS status, race/ethnicity, sex, and SES. Model 2 represented self-efficacy, after controlling for person inputs and background environmental influences. Self-efficacy variables included math self-efficacy, science self-efficacy, and STEM GPA. Model 3 examined school counseling access, after controlling for the variables in the previous two models. School counseling access variables were school counselor caseload and school counselor percentage of time spent on college-readiness counseling. Table 1 displays the model steps and variables.
Table 1
Logistic Regression Model Steps

Results
The aim of the current study was to examine the predictors of STEM major attainment and persistence, including school counselor caseload ratio and percentage of time spent on college-readiness counseling. First, preliminary analysis included running descriptive statistics and a correlation matrix.
Preliminary Analysis
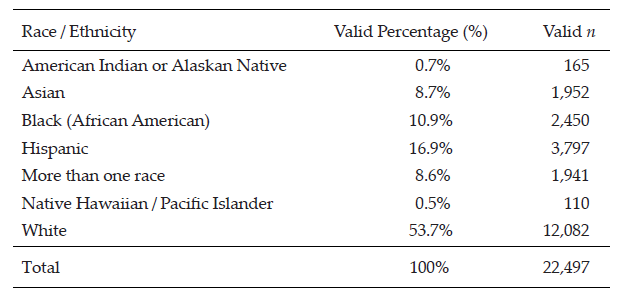
Frequencies and percentages on the variables’ unweighted, valid data (i.e., data before weights were applied and not including missing data) are reported in this section. First, descriptive statistics on person inputs and background environmental influences (i.e., student demographics) were collected. A total of 56.4% (n = 9,468) of the valid sample were FGCS, and 43.6% (n = 7,314) were non-FGCS. A total of 50.9% (n = 11,973) of the sample were identified as female, and the remaining 49% (n = 11,524) as male. The continuous SES variable ranged from −1.93 to 2.88, with a mean score of 0.05 (SD = 0.78). For information on participants’ race/ethnicity, see Table 2.
Table 2
Participant Race and Ethnicity Variable Percentages and Frequencies
Math self-efficacy scores ranged from −2.92 to 1.62 (M = 0.0421, SD = 0.96). Science self-efficacy scores ranged from −2.91 to 1.83 (M = .0372, SD = 0.99). In terms of STEM GPA, the range was 0.25 through 4.00, reported in intervals of 0.25 (M = 2.43, SD = 0.93).
The school counselor caseload in the current study had a mean score of 347.65 students (SD = 130), ranging from 2–999. The median was 350. The school counselor percentage of time spent on college-readiness counseling scores ranged from 1–5 (M = 3.37, SD = 0.95). A total of 2.3% (n = 484) chose 5% or less, and 16.2% (n = 3,389) of the sample chose 6%–10%. A total of 33.8% (n = 7,094) indicated 11%–20%, followed by 37.5% (n = 7,867) choosing 21%–50%. Finally, 10.2% (n = 2,132) of the sample chose the more than 50% option.
For the STEM major persistence and attainment variable, 23% (n = 2,658) of the valid sample were enrolled as a STEM major or had attained a STEM degree as of February 2016, and 77% (n = 8,902) were neither enrolled as a STEM major nor had attained a STEM degree as of February 2016.
Bivariate Correlations
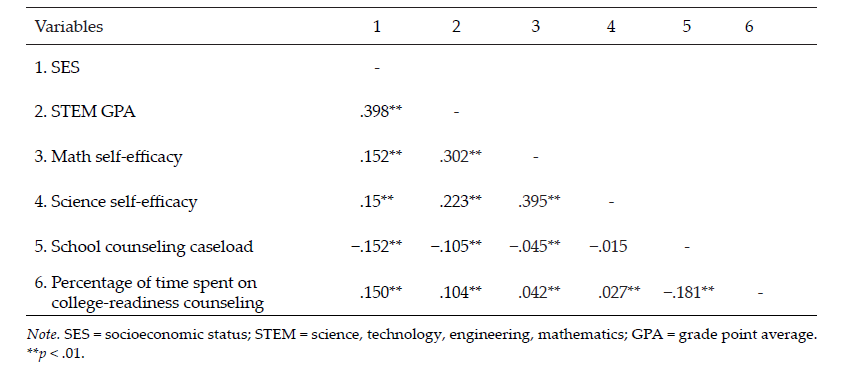
A bivariate correlational analysis of interval and ratio variables in the study allowed for preliminary examination of collinearity and provided information on relationships between the variables of interest. The bivariate correlation matrix indicated no concerns regarding multicollinearity. The correlations contain indications of relationships to school counseling access. For example, school counseling caseload and percentage of time spent on college-readiness counseling were inversely related (r = −.181, p < .01). School counselor caseload was negatively significantly correlated to SES, STEM GPA, and math self-efficacy. School counselor percentage of time spent on college-readiness counseling was positively significantly correlated with SES, STEM GPA, math self-efficacy, and science self-efficacy. See Table 3 for the full results of the bivariate correlations.
Table 3
Bivariate Correlations
Primary Analysis
Next, the results of the sequential logistic regression are presented (see Table 4). The outcome variable is a dichotomous variable of STEM major persistence and attainment and indicated if a student either is or is not enrolled as a declared STEM major in a postsecondary institution or has or has not attained a degree in a STEM field from a postsecondary institution.
Statistical assumptions of the model were assessed. Tolerance (0.26) and VIF values (mean VIF = 1.34) indicated no concerns regarding multicollinearity. The Box-Tidwell test indicated the assumption of a linear relationship between continuous predictors and the logit transform of the outcome variable was met, with nonsignificant p values. Utilizing the balanced repeated replication variance estimation method, 16,007 observations were included in the regression model, with a population size of 1,540,118 and 192 replications.
Table 4
Logistic Regression Model Predicting STEM Major Attainment and Persistence
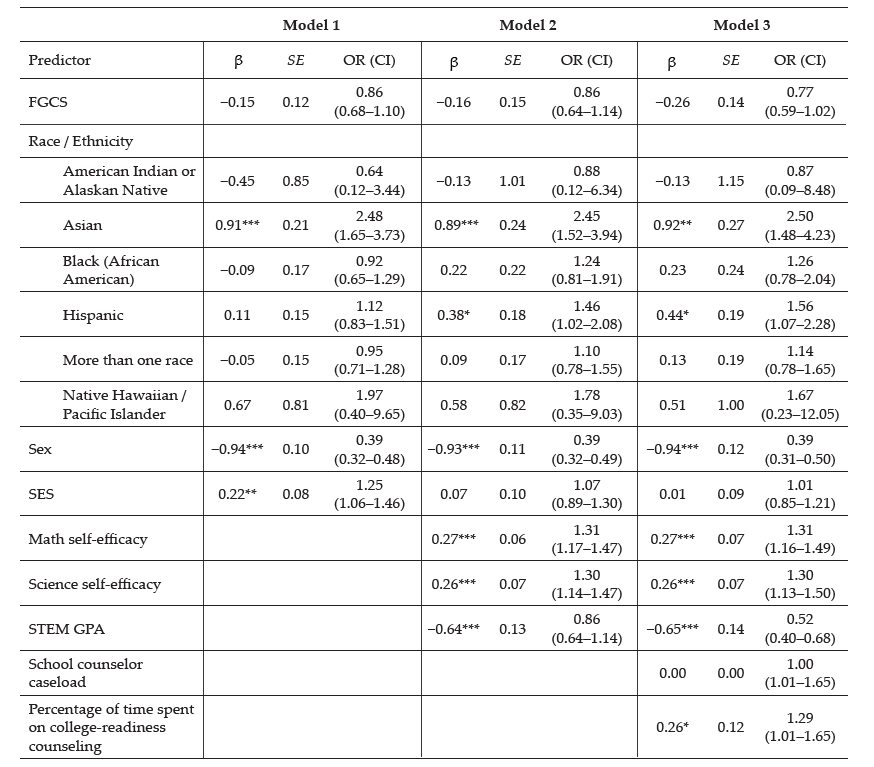
Note. Model 1 = person inputs and background environmental influences (first-generation college student [FGCS], race/ethnicity, sex, socioeconomic status [SES]), without any controls; Model 2 = person inputs and background environmental influences, and self-efficacy variables (math self-efficacy, science self-efficacy, and STEM grade point average [GPA]); Model 3 = person inputs and background environmental influences, self-efficacy variables, and proximal environmental influences (school counselor caseload and percentage of time spent on college-readiness counseling). Reference categories: FGCS = non-FGCS; Sex = male; Race/ethnicity = White; STEM GPA = 3.0–4.0; Percentage of time spent on college-readiness counseling = less than 21%.
*p < .05. **p < .01. ***p < .001.
Model 1 was significant, F(9, 189) = 12.49, p < .001. McFadden’s R Square was 0.0506, indicating that the model explains 5.06% of the variance outcomes. This model indicated that SES significantly predicted STEM major attainment and persistence (β = 0.22, p < .001). In addition, female students were less likely than males to report STEM major attainment and persistence (β = −0.94, p < .001). Asian students were significantly more likely than White students to report STEM major attainment and persistence (β = 0.91, p < .001).
Model 2 was significant, F(12, 185) = 19.03, p < 0.001, McFadden’s R Square = 0.0966. STEM GPA significantly predicted STEM major attainment and persistence, with students with GPAs ranging from 0.25–2.75 being significantly less likely to report STEM attainment and persistence compared to students with GPAs of 3.00–4.00 (β = −0.64, p < .001). Both math self-efficacy (β = 0.27, p < .001) and science self-efficacy (β = 0.26, p < .001) were significant predictors of STEM major attainment and persistence, with increases in these variables resulting in higher odds of the outcome. Female sex and Asian race identity remained significant, while SES was no longer significant.
Model 3 was significant, F(14, 178) = 15.90, p < .001, McFadden’s R Square = 0.1005. For Model 3, the Archer–Lemeshow goodness-of-fit test was not significant, and the adjusted Wald test was significant, indicating good model fit. In this model, school counselor percentage of time spent on college-readiness counseling predicted student STEM major attainment and persistence, with 21% or more time spent on college-readiness counseling being more likely to result in the outcome, compared to 20% or less time spent on college-readiness counseling (β = .26, p < .05). School counselor’s caseload was not significant. Female sex, Asian race identity, STEM GPA, math self-efficacy, and science self-efficacy all remained significant predictors in the final model. The model correctly classified 77.34% of the cases, with higher specificity (95.94%) than sensitivity (19.40%).
Discussion
A sequential logistic regression analysis provided the means for exploration of the research question: Do school counselor caseload and percentage of time spent on college-readiness counseling predict STEM major attainment and persistence? Sequential logistic regression allowed for sociocultural context to be considered in the prediction of STEM career–related performance. This is important because the structure of opportunity (e.g., SES, education access, social support), socialization of gender roles, and other societal and family norms influence abilities, self-efficacy, outcome expectations, and goals within SCCT (Lent & Brown, 1996). The first model included person inputs and background environmental influences (Lent et al., 1994), including FGCS status, race/ethnicity, sex, and SES. Students of Asian race/ethnicity had higher odds of persisting in a STEM major or attaining a degree, compared to the White student reference group, which echoes previous research (Chen, 2013; Mau, 2016). SES also predicted the outcome, with students of higher SES having higher odds of STEM persistence and attainment, which is aligned with previous research on students’ SES status and STEM outcomes (Chen, 2013). Finally, female students had lower odds of persisting in a STEM major or attaining a STEM degree than male students in the model; this gender disparity in STEM academic and career-related outcomes has also been noted in the literature (Mau, 2016).
The second model extended the investigation of predictors of STEM major attainment and persistence to include self-efficacy variables (i.e., math self-efficacy, science self-efficacy) and STEM high school GPA, in addition to still accounting for the person inputs and background environmental influences. Within this second model, Asian-identifying students and female students held the same patterns of significance as in the first model, which was that Asian-identifying students had higher odds of attaining or persisting, while female students had lower odds. When accounting for the self-efficacy variables, Hispanic-identifying students then showed significantly higher odds of persisting in a STEM major and attaining a STEM degree. Previous research does not report higher odds of Hispanic student STEM major persistence and attainment (Mau, 2016; NSF, 2021). However, this result in the model suggests that when Hispanic students have equitable math self-efficacy, science self-efficacy, and STEM GPAs, their opportunity for STEM success is increased, which has been reflected in an SCCT academic persistence model with Latinx engineering student participants (Lee et al., 2015). STEM self-efficacy is an important subject for school counselors to address with students (Falco, 2017), given its influential role in STEM outcomes (Mau & Li, 2018; Shaw & Barbuti, 2010).
The second model demonstrated that as math self-efficacy and science self-efficacy scores increased, the odds of a student persisting in a STEM major or attaining a STEM degree increased significantly. Further, students with higher STEM GPAs in high school were more likely to persist in STEM majors or attain a STEM degree. This is aligned with SCCT, which suggests previous learning experiences and prior accomplishments have a positive effect on career-related outcomes (Lent & Brown, 1996). Previous research (Chen, 2013) has also suggested that lack of preparation in advanced STEM courses in high school leads to more STEM major attrition.
The final model included all previous variables and added the two school counseling access variables: school counselor caseload and school counselor percentage of time spent on college-readiness counseling. Variables that remained significant in the model, in the same directionality of odds of the outcome, were: Asian race/ethnicity, Hispanic race/ethnicity, sex, math self-efficacy, science self-efficacy, and high school STEM GPA. The final model showed women were less likely to persist in STEM majors or attain a STEM degree even when accounting for the access to school counseling variables. This gender disparity is unfortunately reflective of the extant literature on STEM outcomes (Chen, 2013). It also perhaps speaks to the barriers school counselors face when working with historically underrepresented students surrounding STEM (Cabell et al., 2021), such as a lack of encouragement from educators for girls to pursue STEM endeavors (Grossman & Porche, 2014).
In the current study, school counselor caseload was not significant in the model. This finding is not aligned with previous research that found the addition of each school counselor to a school’s staff was associated with a 10% increase in 4-year college-going rates (Hurwitz & Howell, 2014), which suggests the influence of caseload on student postsecondary outcomes, as typically more school counselors on staff results in lower caseloads. However, it is important to note that school counselor caseload did have a significant relationship with the percentage of time spent on college-readiness counseling in the current study, with more students on a caseload resulting in less time spent on college-readiness counseling, according to the bivariate correlation analysis.
School counselor percentage of time spent on college-readiness counseling was significant in the final model, and the results indicated that students who have a school counselor who spends at least the national average of time on college-readiness counseling (i.e., 21%) have higher odds of persisting in STEM majors or attaining a STEM degree. Students who have a school counselor who spends 21% or more of their time on college-readiness counseling have 29% higher odds of STEM major persistence and attainment 3 years post–high school graduation. This finding is novel in the literature. School counseling and STEM counseling is a relatively new area of research in the school counseling literature (Falco, 2017; Schmidt et al., 2012). The current study’s finding on the impact of school counselors’ college-readiness counseling on STEM outcomes extends existing research that has noted the importance of school counselors’ role in STEM counseling (Falco, 2017; Falco & Summers, 2019; Shillingford et al., 2017).
Implications
School counselors can use the results of this study to inform their STEM education–focused college-readiness counseling work. A promising result of the study was that school counselors’ percentage of time spent on college-readiness counseling was predictive of STEM major attainment and persistence. Although there were still inequities in which students were achieving this outcome, including female students. This is helpful information to lead school counselors to target intervention efforts with girls. For instance, girls may benefit from more STEM-focused occupational information and verbal persuasion (i.e., encouragement) from school counselors. These results indicate that school counselors should increase their knowledge and awareness of the barriers their female students are facing related to STEM and seek to correct those barriers. Barriers can include school climate, which school counselors can address through both the messages they themselves and all school staff are sending to their female students about STEM. In terms of consultation, it has been suggested school counselors should play an important role in working with STEM teachers to develop curricula that are unbiased and culturally sensitive to the needs of female and minority students, and the results of the study show the long-lasting effects of how a ninth-grade student perceives their self-efficacy in math and science, supporting this suggestion (Mau, 2016).
Additionally, high school STEM GPA was predictive of persisting and attaining a STEM degree. School counselors encourage high achievement from all students, and this result does not suggest that school counselors should focus their STEM career exploration on just those students who have higher STEM GPAs, assuming those with lower STEM GPAs will not want to enroll as STEM majors in college or cannot be successful once there. All students, regardless of STEM GPA, should receive STEM counseling opportunities. School counselors should also strive to create an environment that is inclusive for all students to be successful in STEM. Further, school counselors can connect their students to the resources to support their success in STEM coursework.
Math and science self-efficacy were important predictive factors of persistence and attainment in a STEM degree, and these areas of self-efficacy can be targeted through interventions with students; previous literature has provided suggestions on how school counselors can do so (Falco, 2017; Schmidt et al., 2012; Shillingford et al., 2017). Developing STEM self-efficacy is important, because when this was held constant, there were no students of different races/ethnicities who were at lower odds of persisting and attaining a STEM degree, nor did SES have an influence on outcomes. School counselors must remain vigilant of the structural inequalities underrepresented students face and remove these barriers (Wolniak et al., 2016).
The results of this study also emphasize the importance of counselor educators intentionally discussing STEM career development in the career counseling and other school counseling curriculum. Research has shown school counselors do not feel knowledgeable about careers in the STEM fields and desire more STEM content information to inform their work (Cabell et al., 2021; Hall et al., 2011). STEM counseling within the school counselor repertoire is a relatively new topic (Schmidt et al., 2012), and counselor educators must be aware of this counseling area and incorporate it into their curriculum. Additionally, the results of this study support the need for collaborations between university counseling programs and neighboring school districts to increase counseling access and improve underrepresented students’ STEM outcomes. Finally, both counselor educators and school counselors can use the results of this study, and the many others that have proven the effectiveness of school counseling, to advocate for lower counselor-to-student ratios and more funding for school counselors.
Limitations and Future Research
There are limitations to utilizing secondary analysis of existing data. Specifically, researchers are not privy to selection of the variables and the researchers’ bias can influence which variables are selected to study an outcome; there are many more variables in this dataset which could be included for an exploration of the research question (Cheng & Phillips, 2014). However, the use of the NCES-led HSLS:09 dataset allowed for an extensive number of variables for a massive longitudinal study (NCES, 2020a). A potential area for future exploration in this model could also be school counselors’ self-efficacy in college counseling and STEM counseling and how that impacts students’ outcomes. Further, causal inferences should not be assumed in logistic regression models; probability in correctly predicting an outcome does not mean that these variables cause the outcomes (Tabachnick & Fidell, 2013).
Future research studies could utilize multilevel modelling methods to account for school-level variables, such as staff-to-student ratio, percentage of students on free-and-reduced lunch, and geographic area. This would further investigate systemic influences on access to school counseling and student outcomes and could have the potential to increase the percentage of variance accounted for by the models. Additionally, there has recently been follow-up data added to the HSLS:09 dataset, which includes postsecondary transcripts; this study could be replicated with this data.
Research on school counselors and STEM is growing and should be continued. For instance, researchers have explored school counselors’ experiences regarding STEM and STEM counseling (Cabell et al., 2021; Shillingford et al., 2017). Quantitative research surrounding this topic is needed as well to measure differences in STEM counseling allocation and student STEM outcomes as a result of school counselors’ preparation and efficacy in this area. Finally, an understanding of how counselor education programs are and are not preparing their students to engage in college-readiness counseling and STEM counseling is warranted.
Conclusion
This study provides encouraging results regarding the impact of school counselors’ college-readiness counseling on students’ STEM major attainment and persistence. Results detailed how science and math self-efficacy had strong predictive power on STEM outcomes, which informs school counseling practice. Through increased training in college-readiness counseling and STEM counseling in school counseling training programs, and continued attention to a holistic model of college readiness, school counselors can continue to play an integral role in all students’ college and STEM readiness through providing college-readiness counseling (Gilfillan, 2017; Schmidt et al., 2012).
Conflict of Interest and Funding Disclosure
Data collected and content shared in this article
were part of a dissertation study, which was
awarded the 2021 Dissertation Excellence Award
by the National Board for Certified Counselors.
References
American School Counselor Association. (2019). The ASCA national model: A framework for school counseling programs (4th ed.).
Bandura, A. (1986). Social foundations of thought and action: A social cognitive theory. Prentice-Hall.
Bandura, A. (1994). Self-efficacy. In V. S. Ramachaudran (Ed.), Encyclopedia of human behavior (Vol. 4, pp. 71–81). Academic Press.
Belser, C. T., Shillingford, M. A., Daire, A. P., Prescod, D. J., & Dagley, M. A. (2018). Factors influencing undergraduate student retention in STEM majors: Career development, math ability, and demographics. The Professional Counselor, 8(3), 262–276. https://doi.org/10.15241/ctb.8.3.262
Brown, S. D., & Lent, R. W. (1996). A social cognitive framework for career choice counseling. The Career Development Quarterly, 44(4), 354–366. https://doi.org/10.1002/j.2161-0045.1996.tb00451.x
Cabell, A. L., Brookover, D., Livingston, A., & Cartwright, I. (2021). “It’s never too late”: High school counselors’ support of underrepresented students’ interest in STEM. The Professional Counselor, 11(2), 143–160. https://doi.org/10.15241/alc.11.2.143
Cataldi, E. F., Siegel, P., Shepherd, B., & Cooney, J. (2014). Baccalaureate and beyond: A first look at the employment experiences and lives of college graduates, 4 Years On (B&B:08/12) (NCES 2014-141). National Center for Education Statistics, Institute of Education Sciences, U.S. Department of Education. https://nces.ed.gov/pubs2014/2014141.pdf
Chen, X. (2013). STEM attrition: College students’ paths into and out of STEM fields (NCES 2014-001). National Center for Education Statistics, Institute of Education Sciences, U.S. Department of Education.
https://nces.ed.gov/pubs2014/2014001rev.pdf
Cheng, H. G., & Phillips, M. R. (2014). Secondary analysis of existing data: Opportunities and implementation. Shanghai Archives of Psychiatry, 26(6), 371–375. https://doi.org/10.11919/j.issn.1002-0829.214171
Clinedinst, M., & Koranteng, A.-M. (2017). 2017 state of college admission. National Association for College
Admission Counseling. https://bit.ly/3BNizx8
Duprey, M. A., Pratt, D. J., Jewell, D. M., Cominole, M. B., Fritch, L. B., Ritchie, E. A., Rogers, J. E., Wescott, J. D., & Wilson, D. H. (2018). High School Longitudinal Study of 2009 (HSLS:09) base-year to second follow-up data file documentation (NCES 2018-140). National Center for Education Statistics, Institute of Education Sciences, U.S. Department of Education. https://nces.ed.gov/pubs2018/2018140.pdf
Engberg, M. E., & Gilbert, A. J. (2014). The counseling opportunity structure: Examining correlates of four-year college-going rates. Research in Higher Education, 55(3), 219–244.
Falco, L. D. (2017). The school counselor and STEM career development. Journal of Career Development, 44(4), 359–374. https://doi.org/10.1177/0894845316656445
Falco, L. D., & Summers, J. J. (2019). Improving career decision self-efficacy and STEM self-efficacy in high school girls: Evaluation of an intervention. Journal of Career Development, 46(1), 62–76.
https://doi.org/10.1177/0894845317721651
Gilfillan, B. H. (2017). School counselors and college readiness counseling. Professional School Counseling, 21(1). https://doi.org/10.1177/2156759X18784297
Grossman, J. M., & Porche, M. V. (2014). Perceived gender and racial/ethnic barriers to STEM success. Urban Education, 49(6), 698–727. https://doi.org/10.1177/0042085913481364
Hall, C., Dickerson, J., Batts, D., Kauffmann, P., & Bosse, M. (2011). Are we missing opportunities to encourage interest in STEM fields? Journal of Technology Education, 23(1), 32–46. https://files.eric.ed.gov/fulltext/EJ96
5337.pdf
Hurwitz, M., & Howell, J. (2014). Estimating causal impacts of school counselors with regression discontinuity designs. Journal of Counseling & Development, 92(3), 316–327. https://doi.org/10.1002/j.1556-6676.2014.00159.x
Ingels, S. J., & Dalton, B. (2013). High School Longitudinal Study of 2009 (HSLS:09) first follow-up: A first look at fall 2009 ninth graders in 2012 (NCES 2014-360). National Center for Education Statistics, Institute of Education Sciences, U.S. Department of Education. https://nces.ed.gov/pubs2014/2014360.pdf
Lavrakas, P. J. (Ed.). (2008). Encyclopedia of survey research methods (Vols. I–II). SAGE.
Lee, H.-S., Flores, L. Y., Navarro, R. L., & Kanagui-Muñoz, M. (2015). A longitudinal test of social cognitive career theory’s academic persistence model among Latino/a and White men and women engineering students. Journal of Vocational Behavior, 88, 95–103. https://doi.org/10.1016/j.jvb.2015.02.003
Lent, R. W. (2005). A social cognitive view of career development and counseling. In S. D. Brown & R. W. Lent (Eds.), Career development and counseling: Putting theory and research to work (pp. 101–127). Wiley.
Lent, R. W., & Brown, S. D. (1996). Social cognitive approach to career development: An overview. The Career Development Quarterly, 44(4), 310–321. https://doi.org/10.1002/j.2161-0045.1996.tb00448.x
Lent, R. W., Brown, S. D., & Hackett, G. (1994). Toward a unifying social cognitive theory of career and academic interest, choice, and performance. Journal of Vocational Behavior, 45(1), 79–122.
https://doi.org/10.1006/jvbe.1994.1027
Lent, R. W., Brown, S. D., & Hackett, G. (2000). Contextual supports and barriers to career choice: A social cognitive analysis. Journal of Counseling Psychology, 47(1), 36–49. https://doi.org/10.1037/0022-0167.47.1.36
Lent, R. W., Miller, M. J., Smith, P. E., Watford, B. A., Lim, R. H., & Hui, K. (2016). Social cognitive predictors of academic persistence and performance in engineering: Applicability across gender and race/ethnicity. Journal of Vocational Behavior, 94, 79–88. https://doi.org/10.1016/j.jvb.2016.02.012
Lips, H. M. (2020). Sex and gender: An introduction (7th ed.). Waveland Press.
Malin, J. R., Bragg, D. D., & Hackmann, D. G. (2017). College and career readiness and the Every Student Succeeds Act. Educational Administration Quarterly, 53(5), 809–838. https://doi.org/10.1177/0013161X17714845
Mau, W.-C. J. (2016). Characteristics of US students that pursued a STEM major and factors that predicted their persistence in degree completion. Universal Journal of Educational Research, 4(6), 1495–1500.
https://doi.org/10.13189/ujer.2016.040630 https://files.eric.ed.gov/fulltext/EJ1103170.pdf
Mau, W.-C. J., & Li, J. (2018). Factors influencing STEM career aspirations of underrepresented high school students. The Career Development Quarterly, 66(3), 246–258. https://doi.org/10.1002/cdq.12146
Meyers, L. S., Gamst, G., & Guarino, A. J. (2017). Applied multivariate research: Design and implementation
(3rd ed.). SAGE.
Mohr-Schroeder, M. J., Cavalcanti, M., & Blyman, K. (2015). STEM education: Understanding the changing landscape. In A. Sahin (Ed.), A practice-based model of STEM teaching: STEM Students on the Stage (SOS) (pp. 3–14). Sense. https://doi.org/10.1007/978-94-6300-019-2
National Center for Education Statistics. (2020a). High School Longitudinal Study of 2009 (HSLS:09) [Data set]. Institute of Education Sciences. https://nces.ed.gov/surveys/hsls09/hsls09_data.asp
National Center for Education Statistics. (2020b). High School Longitudinal Study of 2009 (HSLS:09). https://nce
s.ed.gov/surveys/hsls09/index.asp
National Center for Education Statistics. (2020c). College enrollment rates. Institute of Education Sciences.
https://nces.ed.gov/programs/coe/indicator_cpb.asp
National Science Foundation. (2021). Women, minorities, and persons with disabilities in science and engineering: 2021. National Center for Science and Engineering Statistics Special Report NSF 19-304. https://www.ns
f.gov/statistics/wmpd
Rittmayer, A. D., & Beier, M. E. (2009). Self-efficacy in STEM. In B. Bogue & E. Cady (Eds.), Applying research to practice (ARP) Resources. http://aweonline.org/selfefficacy_002.html
Savitz-Romer, M. (2012). The gap between influence and efficacy: College readiness training, urban school counselors, and the promotion of equity. Counselor Education and Supervision, 51(2), 98–111, 158.
https://doi.org/10.1002/j.1556-6978.2012.00007.x
Schmidt, C. D., Hardinge, G. B., & Rokutani, L. J. (2012). Expanding the school counselor repertoire through STEM-focused career development. The Career Development Quarterly, 60(1), 25–35.
https://doi.org/10.1002/j.2161-0045.2012.00003.x
Shaw, E. J., & Barbuti, S. (2010). Patterns of persistence in intended college major with a focus on STEM majors. NACADA Journal, 30(2), 19–34. https://doi.org/10.12930/0271-9517-30.2.19
Shillingford, M. A., Oh, S., & Finnell, L. R. (2017). Promoting STEM career development among students and parents of color: Are school counselors leading the charge? Professional School Counseling, 21(1b), 1–11. https://doi.org/10.1177/2156759X18773599
Sperandei, S. (2014). Understanding logistic regression analysis. Biochemia Medica, 24(1), 12–18.
https://doi.org/10.11613/BM.2014.003
Tabachnick, B. G., & Fidell, L. S. (2013). Using multivariate statistics (6th ed.). Pearson.
Tsupros, N., Kohler, R., & Hallinen, J. (2009). STEM education: A project to identify the missing components [Summary report]. Intermediate Unit 1: Center for STEM Education and Leonard Gelfand Center for Service Learning and Outreach, Carnegie Mellon University, Pennsylvania.
U.S. Department of Education. (2010). A blueprint for reform: The reauthorization of the Elementary and Secondary Education Act. Office of Planning, Evaluation and Policy Development. https://www.ets.org/s/education
_topics/ESEA_Blueprint.pdf
Vilorio, D. (2014). STEM 101: Intro to tomorrow’s jobs. Occupational Outlook Quarterly, Spring, 58, 3–12.
https://www.bls.gov/careeroutlook/2014/spring/art01.pdf
The White House, Office of Science and Technology Policy, National Science and Technology Council. (2018). Charting a course for success: America’s strategy for STEM education. Office of Science and Technology Policy. https://www.energy.gov/sites/default/files/2019/05/f62/STEM-Education-Strategic-Plan-2018.pdf
Wolniak, G. C., Wells, R. S., Engberg, M. E., & Manly, C. A. (2016). College enhancement strategies and socioeconomic inequality. Research in Higher Education, 57(3), 310–334.
https://doi.org/10.1007/s11162-015-9389-4
Xue, Y., & Larson, R. C. (2015). STEM crisis or STEM surplus? Yes and yes. Monthly Labor Review. U.S. Bureau of
Labor Statistics. https://doi.org/10.21916/mlr.2015.14
Dana L. Brookover, PhD, NCC, is a licensed school counselor and an assistant professor at the University of Scranton. Correspondence may be addressed to Dana L. Brookover, McGurrin Hall Room 435, McGurrin Hall, The University of Scranton, Scranton, PA 18510, brookoverdl@gmail.com.
Apr 1, 2021 | Volume 11 - Issue 2
Autumn L. Cabell, Dana Brookover, Amber Livingston, Ila Cartwright
The purpose of this study was to contribute to the literature surrounding school counselors and their support of underrepresented high school students who are interested in science, technology, engineering, and math (STEM). The influence of context on school counseling was also explored, in particular practicing during the COVID-19 pandemic. Through this phenomenological study, nine high school counselors were individually interviewed, and four themes emerged. These themes were: (a) professional knowledge surrounding issues of diversity in STEM, (b) training related to the needs of underrepresented students in STEM, (c) active engagement in supporting underrepresented students’ STEM career interests, and (d) barriers related to supporting underrepresented students’ STEM interests. This article includes implications for (a) how school counselors can support underrepresented students’ STEM interests, particularly during the COVID-19 pandemic; (b) how counselor educators can contribute to STEM-related research and training; and (c) how school administrators can support school counselors’ STEM initiatives.
Keywords: STEM, school counseling, underrepresented students, high school, COVID-19
The science, technology, engineering, and math (STEM) fields in the United States comprise a large and growing sector of the economy (National Science and Technology Council [NSTC], 2018). Currently, there are more than 9 million people employed in STEM careers (U.S. Bureau of Labor Statistics [BLS], 2020). This is approximately 6% of the United States workforce (BLS, 2020). According to the BLS (2020), computer science, engineering, and physical science occupations; managerial and postsecondary teaching occupations related to those areas; and sales occupations requiring scientific knowledge at the postsecondary level are considered STEM occupations. STEM occupations require the knowledge and skills to solve problems, make sense of information, and gather and evaluate evidence to make decisions (U.S. Department of Education [U.S. ED], n.d.). In order to meet the demands of the evolving workforce and society, the United States needs students who are fluent in STEM fields and are pursuing careers in STEM (U.S. ED, n.d.).
The demand for professionals and employees with STEM skill sets is a national priority (NSTC, 2018). Estimates indicate that there will be a shortage of over 1 million STEM workers (Xue & Larson, 2015), and the need for workers will grow by 8% before 2030 (BLS, 2020). In contrast, non-STEM occupations are only projected to grow by 3% before 2030 (BLS, 2020). Because of the need for professionals with STEM skill sets, choosing to pursue a career in the STEM sector leads to the potential for positive job marketability. In addition, students who major in STEM programs during college may earn a higher salary upon graduation than other students (Cataldi et al., 2014; Vilorio, 2014). However, not all students have equitable opportunities to pursue careers in STEM.
The Need for Diversity in STEM
Diversity in STEM continues to be a concern in the United States (National Science Foundation, 2019). Beginning in high school, fewer women and minorities expect to have a career in STEM at age 30 (Mau & Li, 2018). Then, in college, significantly more men than women declare STEM majors and significantly more Asian and White students declare STEM majors (Mau, 2016). Although women now make up over half of the overall workforce, they are underrepresented in certain STEM sectors, such as computer jobs and engineering (Funk & Parker, 2018). Relatedly, in 2015–2016, more bachelor’s degrees were awarded to females (58%) than males (42%), yet females only made up 36% of bachelor’s degrees in STEM fields (National Center for Education Statistics [NCES], 2019). Additionally, the gender wage gap is wider in the STEM fields than in non-STEM jobs (Funk & Parker, 2018).
Further, Black, Latinx, and Native American workers are underrepresented in STEM occupations when compared to White and Asian workers (Funk & Parker, 2018; Mau, 2016). Though racial minorities are gradually becoming more represented in STEM fields, there is still more work to be done. For example, in 2015–2016, White students were awarded approximately 90% of the bachelor’s degrees in STEM fields (NCES, 2019). The percentages of Latinx (15%), Black (12%), and Native American (14%) students who received degrees in STEM was disproportionately lower than that of White students.
These gender and racial disparities in STEM begin even before students enter college. High school is a critical timepoint to address gender and racial disparities in STEM. High school provides students with an opportunity to engage in higher-level STEM coursework and gain self-efficacy in their STEM skills and abilities. Chen (2013) suggested that when students do not have the opportunity to engage with higher-level coursework in STEM, they are less likely to complete college degrees in STEM. Further, Grossman and Porche (2014) explained that during the high school years, encouragement to pursue STEM coursework is critical to developing students’ STEM self-efficacy. Mau and Li (2018) found that ninth grade students with higher math and science self-efficacy were more likely to have STEM career expectations and aspirations.
However, girls and underrepresented minorities in K–12 are more likely to experience stereotype threat (i.e., anxiety about their performance or ability based on negative stereotypes) and less likely to be enrolled in advanced STEM coursework during high school (Curry & Shillingford, 2015; Hamilton et al., 2015). This results in gaps in advanced STEM skills and a lack of further interest in STEM careers. Thus, professional school counselors must address the inequities in opportunity for their students through targeted STEM career interventions. Often, high school is a student’s last opportunity to develop their interest in STEM careers (Falco & Summers, 2019; Schmidt et al., 2012; Shillingford et al., 2017).
School Counselors and STEM
Under their role as defined by the American School Counselor Association (ASCA) National Model (2012), professional school counselors play an integral part in utilizing career counseling to support and encourage students to pursue STEM education and careers (Schmidt et al., 2012). Falco (2017) provided a conceptual model for school counselors to guide their STEM academic and career support with their students, including: (a) encouraging students to take advanced math and science courses, (b) providing classroom instruction on the benefits of pursuing STEM education, and (c) improving self-efficacy through providing mentoring and small group counseling opportunities. Other suggested roles for professional school counselors in STEM counseling involve ensuring equitable gender and racial ethnic ratios in STEM classes, integrating STEM knowledge into goal setting, and involving parents and guardians in academic and career planning (Schmidt et al., 2012). Although the topic of STEM counseling within the school counseling profession is still emerging, school counselors and researchers have highlighted the importance of working with girls and underrepresented racial minorities regarding STEM pursuits (Falco & Summers, 2019; Shillingford et al., 2017).
School Counselors and STEM for Girls and Underrepresented Racial Minorities
In order to provide equitable and anti-racist school counseling services, professional school counselors must be knowledgeable and aware of the factors perpetuating the opportunity gaps in STEM for girls and underrepresented minorities. Potential reasons for the opportunity gaps in STEM higher education include: (a) young people not being engaged in higher-level STEM coursework in high school, (b) inability to meet the financial or time commitment required by STEM programs, and (c) motivation and confidence concerns (Chen, 2013). Additionally, starting in adolescence, underrepresented students in the STEM fields also face a lack of support and encouragement and, oftentimes, direct discouragement from educators regarding enrollment in rigorous STEM coursework (Grossman & Porche, 2014).
Unfortunately, underrepresented students are less likely to expect their school counselors to share postsecondary information with them, and school counselors often miss opportunities to improve underrepresented students’ STEM outcomes (Dockery & McKelvey, 2013; Shillingford et al., 2017). Yet, emerging evidence shows that school counselors can impact STEM aspirations in students. For instance, one school counseling intervention that showed promising results in promoting STEM self-efficacy was a career group intervention with adolescent girls, half of whom identified as Latina (Falco & Summers, 2019). The school counseling intervention focused on targeting STEM self-efficacy and career decision self-efficacy. The results indicated that participants in the treatment group improved significantly on both outcomes and even increased those gains 3 months post-intervention when compared to the control group (Falco & Summers, 2019).
In another study, researchers aimed to investigate the influence that school counselors’ leadership had on STEM engagement, their collaboration between parents and students of color, and barriers that inhibited them from giving students more tools and resources to contribute to their success (Shillingford et al., 2017). The school counselors in the study aligned with a leadership style that integrated collaborative and motivational techniques and suggested other school counselors can utilize their leadership style to communicate more effectively with parents and support racially underrepresented students’ STEM aspirations (Shillingford et al., 2017). However, there are barriers surrounding these efforts, including inadequacy of education around STEM for school counselors; challenges with supporting parents, especially parents from marginalized racial identities; and having insufficient resources to benefit students (Shillingford et al., 2017). These studies show that school counselors can target STEM self-efficacy and emphasize school counselors’ roles in promoting STEM career aspirations with racially underrepresented students. However, the current context of the COVID-19 pandemic should be taken into consideration when surveying the current climate of STEM counseling with students.
COVID-19 and School Counselors
The COVID-19 pandemic has highlighted the inequities within our education system (Aguilar, 2020). For example, there is a digital equity gap, which includes a lack of access to adequate technology or internet, which must be taken into consideration and addressed in the virtual and hybrid learning settings many school divisions have adopted (Aguilar, 2020). During the pandemic, students often come to their virtual learning environments disengaged and having experienced various traumas (Savitz-Romer et al., 2020). These considerations call for flexibility, empathy, and perseverance from educators, including school counselors.
School counselors are trained in promoting students’ social-emotional, academic, and postsecondary development and hence are key to supporting students’ readjustment, learning, and continued college and career readiness progress during this time (Savitz-Romer et al., 2020). The work of the school counselor has not halted, especially with the challenges inherent in transitioning to a new way of school counseling. These challenges during the pandemic have led to less time spent in their usual counseling about social-emotional issues, career development, or postsecondary plans; notably, 50% of school counselors reported they spent less time than usual on career planning, and 25% reported less time spent on college planning (Savitz-Romer et al., 2020). Still, school counselors are pushing forward and adapting their practices to continue their work, including STEM counseling (ASCA, 2021).
Purpose of the Current Study
As reviewed, professional school counselors play a vital role in the development and motivation of students interested in STEM. Shillingford and colleagues (2017) called attention to the necessity of educating school counselors on how to support students of color interested in the STEM fields, as well as the influence of having a collaborative relationship between parents, students, and school counselors to assist with students’ STEM career development and exploration. Although Shillingford et al. emphasized the leadership role school counselors take in impacting the pipeline of students of color in STEM, their work (a) does not address the intersectionality of the race and gender disparities in STEM and (b) does not specifically address the critical, and perhaps last, opportunity for counseling intervention that can take place at the high school level.
Given the need for gender and racial diversity in STEM and the limited literature that emphasizes the role of school counselors in STEM counseling and education, the purpose of this transcendental phenomenological study was to increase understanding of the lived experiences of high school counselors who support girls’ and underrepresented minority students’ interests in STEM. As students begin to prepare for their next step in life, high school is the last chance school counselors have to intervene and influence students who have shown interest in STEM-related careers and minimize potential barriers that may come their way. Thus, the following research questions guided this inquiry: 1) What are the experiences of high school counselors who support girls’ and underrepresented minority students’ STEM interests and career aspirations? and 2) What contexts (including the COVID-19 pandemic) influence high school counselors’ support of girls’ and underrepresented minority students’ STEM interests and career aspirations?
Method
A transcendental phenomenological approach was used to develop understanding of the experiences of high school counselors who support underrepresented students’ STEM career interests and the contexts that influence their support. Transcendental phenomenology is a suitable design when the aim is to discover the essence, or the nature, of a phenomenon, experience, or concept (Moustakas, 1994). Our research team included four members. Our first author, Cabell, is a Black, cisgender female counselor educator. As the primary researcher, her role was to recruit and interview participants and to assist with coding. The research team also included two Black, cisgender female counselor education and supervision doctoral students, Livingston and Cartwright, and one White, cisgender female counselor education doctoral candidate, Brookover. Cabell, Brookover, and Cartwright hold master’s degrees in school counseling. Cabell and Brookover previously worked as high school counselors and Cartwright worked as an elementary school counselor at the time of the study. In addition, Cabell has professional experience providing career counseling to undergraduate engineering students. Livingston earned a master’s degree in college counseling and has professional experience working with diverse populations of college students.
Sample
The recommended sample size for phenomenological qualitative research is 5–25; thus, participants were recruited with this range in mind (Creswell & Poth, 2017), using purposeful sampling. Criteria for inclusion were school counselors or school counselor interns who worked in a high school within the past 2 years. A total of nine school counselors participated in this study.
Participants were seven school counselors who worked in a high school at the time of the study, one school counselor who worked in a high school within the past 2 years, and one college counselor who worked in a high school at the time of the study. Participants were racially diverse with six identifying as Black, two identifying as White, and one identifying as Mexican American/Chicano. Regarding gender, seven identified as cisgender women and two identified as cisgender men. Participants’ ages ranged from 26 to 46. In addition, the sample included participants who worked in various states, including two each in California and Virginia; one each in Indiana, Maryland, Michigan, and Washington, D.C.; and one who worked in both Kansas and Missouri. Three participants stated that they worked at a Catholic private high school. As part of their role, all participants stated that they provided career counseling services to students on a weekly basis. Most participants (n = 5) explained that the high school where they worked was diverse with regard to students’ race and gender. Lastly, participants had 4–18 years of experience working as high school counselors. See Table 1 for participant pseudonyms and demographics.
Table 1
Participant Pseudonyms and Demographics
| Pseudonym |
Gender |
Age |
Race |
State |
Years of Experience |
Role and Work Experience |
| Jane |
Female |
38 |
Black |
MD |
7 |
Counselor at a Catholic high school |
| Kate |
Female |
40 |
Black |
CA |
5 |
College counselor at a Catholic high school |
| Christy |
Female |
26 |
Black |
D.C. |
4 |
Counselor at a Catholic high school |
| Lauren |
Female |
37 |
White |
KS/MO |
7 |
Counselor who just switched from
high school to elementary school |
| Dawn |
Female |
30 |
Black |
VA |
4 |
Counselor at a public high school |
| Kelly |
Female |
37 |
Black |
MI |
13 |
Counselor at a public high school |
| Jo |
Male |
46 |
Mexican American/Chicano |
CA |
18 |
Counselor at a public high school |
| Tina |
Female |
35 |
Black |
IN |
4 |
Counselor at a public high school |
| Mark |
Male |
38 |
White |
VA |
6 |
Counselor at a public high school |
Data Collection
First, the study was approved by the university’s IRB. After approval, our first author, Cabell, sent recruitment flyers and emails to high school counselors using social media platforms (e.g., Twitter, Facebook, and LinkedIn) and state and national school counseling listservs (e.g., ASCA SCENE). Volunteers who met the eligibility criteria were encouraged to email Cabell in order to schedule a virtual interview through Zoom. Volunteers confirmed via email that they were a school counselor or school counseling intern at a high school within the past 2 years. Then, volunteers were sent the informed consent form and information on how to schedule their interview. Once scheduled, participants were emailed a Zoom link and directions on how to start their interview. Each interview lasted approximately 30–45 minutes and was audio-recorded.
At the beginning of each semi-structured interview, participants were asked demographic questions. Cabell developed interview questions based on the literature regarding (a) school counselors’ involvement in STEM education, (b) the underrepresentation of girls and racial minorities (e.g., Black, Latinx, and Native American) in STEM, and (c) the impact of COVID-19 on school counseling and K–12 education. The interview included 11 questions (see Appendix for the full list). Example interview questions included: What is your understanding of the issues of diversity in STEM? What has been your experience in promoting STEM careers to underrepresented students? What barriers do you face in promoting STEM careers to underrepresented students? and How has the COVID-19 pandemic impacted your role in supporting underrepresented students’ STEM career aspirations and interests? Following each interview, the audio recordings were transcribed using a website (Rev.com) and checked for accuracy by both Cabell and the participants. Cabell reviewed the transcripts for accuracy and made any changes due to typographical errors. She then emailed the transcripts to participants to review and make any changes. Two participants identified typographical errors in their transcript and emailed Cabell with edits.
Data Analysis
Data from the interview transcripts were analyzed. First, the raw data from the transcripts were examined to note significant quotes (i.e., horizontalization). Each transcript was reviewed individually by Cabell and Cartwright for exemplary quotes related to the research questions. Then, clusters of meaning were developed from these quotes and compiled into themes. These themes were used to develop descriptions of the participants’ experiences and explain how contextual factors influenced their support of underrepresented students’ STEM career interests and aspirations.
Trustworthiness
Trustworthiness is critical to establishing the validity of qualitative research; thus, several measures were implemented (Maxwell, 2005). First, in order to set aside personal biases, experiences, and feelings regarding the purpose of the research, all members of our research team engaged in bracketing our own experiences (i.e., epoché) before beginning this research (Creswell & Poth, 2017; Moustakas, 1994). Bracketing was completed in the form of concept maps and journaling. We individually bracketed our potential biases and then discussed our process with the team. Potential biases that were discussed included: (a) the impact of our first author’s experience providing career counseling to engineering undergraduate students, (b) our race and gender, and (c) our prior school counseling experience with underrepresented minorities.
In addition, throughout each semi-structured interview, Cabell completed check-ins to ensure understanding of the participant’s experience and perspective. Also, after each interview was transcribed, participants were sent their transcripts for member checking. Any inaccuracies in the transcript were changed based on the participant’s responses. Only transcripts that were reviewed by the participant were analyzed. Next, Cabell and Cartwright independently coded each transcript. Then, we established group consensus for all themes and exemplary quotes. Lastly, after the codebook was developed with themes and participant quotes, we sent the codebook to two counseling graduate students, who served as external auditors after being trained by Cabell on qualitative research and auditing. They reviewed the codebook to identify any discrepancies and ensure the significant quotes, themes, and codes aligned.
Results
We sought to (a) highlight the experiences of high school counselors who support the STEM interests of girls and underrepresented minority students and (b) identify the contexts that impact their ability to support these students, particularly taking into account the COVID-19 pandemic. Specifically, participants reflected on supporting girls; Black, Latinx, and Native American students; and those students at the intersections of both identities (e.g., Black girls, Latinx girls). We identified four themes in the analysis of the high school counselors’ experiences: 1) professional knowledge of issues of diversity in STEM; 2) training related to the needs of underrepresented students in STEM; 3) active engagement or taking an active role in supporting underrepresented students’ STEM career interests; and 4) barriers related to supporting underrepresented students’ STEM interests, including COVID-19, school, administration, students’ self-efficacy, and language.
Theme 1: Professional Knowledge
The first theme of professional knowledge of issues of diversity in STEM encompassed participants’ knowledge of the issues of gender and racial disparities in STEM fields nationally (i.e., representation in STEM occupations) and issues of diversity in STEM at their school (i.e., STEM courses). All participants were aware of the lack of racial and gender diversity in STEM nationally. Jane explained:
People of color, especially Black students, people who identify as female or women are vastly underrepresented in many of the STEM fields. . . . I know that there are many initiatives in K–12 [and] higher education to bring in or recruit or encourage students of color in particular and female students of color to explore STEM.
Similarly, Kate discussed that the STEM fields overall are “moving in a more diverse direction” yet are still dominated by men. She noticed that the majority of the students at her high school who are interested in STEM “are not Black or Brown students, they’re usually everything else.” According to Christy, “there’s a huge gap with our minorities. They don’t have the access to the education of the different jobs in STEM, and how to even reach those positions. . . . It ends up being a cyclical effect.”
Further, Dawn reflected on the lack of representation in STEM fields and the initiatives that she knows aim to diversify the images of STEM professionals. For example, Dawn discussed a social media campaign and stated:
There’s been a cool campaign, like what a scientist looks like. And it’s all of these cool Black women in lab coats. . . . So I’m pretty sure it’s just fighting against stereotypes of who should be in STEM, and what kind of person.
Kelly also spoke to the lack of diversity in STEM, not only as a national issue but also in her high school. Kelly mentioned the STEM opportunity gap: “If students are in STEM programs and they are of color, they don’t really see a lot of support, and they definitely don’t see teachers and staff that look like them.” Likewise, Jo explained that girls in particular “sometimes doubt their ability even though they’re within our top 5% of our school.” Tina acknowledged that there is a need for more girls in STEM and girls of color in STEM nationally, so she explained, “I’ve definitely been pushing my girls, especially my girls of color, my Latinx and my Black girls to definitely go out” and “I often tell them ‘paint engineering with your red lipstick,’ because I think that’s what we need to see is more women out there.”
Theme 2: Training
The second theme of training related to the needs of underrepresented students in STEM was identified through participants’ reflections on formal and informal training opportunities they completed to effectively meet their students’ needs. Some of the participants received informal training with regard to STEM counseling and education. For example, Jane explained that when she first became a school counselor, she “became friends with a few school counselors who were also women of color. And they were . . . fierce advocates for girls of color in the computer science field specifically.” The informal professional development that this group of school counseling peers provided her then led to more formal training on “some of the various tools that are out there, programs that are available, ways in which you can target girls of color and just some of the roadblocks that we as school counselors might run into.” Though Jane received both formal and informal training, she explained, “I’m still learning . . . ways in which we can do better in terms of exposing students, building it into our program, collecting data around it.” Similar to Jane, Mark also had the opportunity to attend both formal and informal training. Mark stated, “I’ve attended the occasional webinar here and there that focuses specifically on that particular demographic.” He also added that he had conversations with “some of the professors and the advisors [at neighboring colleges] within those STEM programs that really helped develop a broader understanding.”
In contrast, many participants (n = 7) could not discuss informal or formal training opportunities with regard to STEM and supporting underrepresented students. Kate explained that she received “nothing in the formal sense” with regard to STEM counseling or education training. Similarly, Christy stated, “I would say formally none, nothing professional regarding development, or seminars, workshops, or anything like that.” However, she did have some informal training because supporting underrepresented students’ STEM interests has been “a conversation that we have had with our counseling department of how to bring different types of professionals into the school and bringing them into the career days.” Dawn expressed that “STEM is such a big field. I still need help learning and understanding everything that STEM offers.” Sharing a similar sentiment in needing to know more, Tina explained, “I wish I knew more. . . . It’s just, I want to know more. I want to be able to support them. My goodness.”
Theme 3: Active Engagement
The third theme of active engagement in supporting underrepresented students’ STEM career interests emphasized the roles the high school counselors took to support students with STEM career interests. Many participants recognized their role as high school counselors in providing students with exposure to STEM career fields and supporting students’ prior knowledge of STEM. Embedded into the interviews with participants was the role of the school counselor and STEM. Christy stated, “It’s really our role to bridge that gap and make the connections that may not have been made previously, or the students might not have had access to before.” Mark shared his role in optimizing students’ strengths:
“Every student is going to present his or her own set of talents and abilities. . . . it’s my job to make sure that I can help them recognize what those talents and abilities are and help them cultivate a passion.”
Participants also took pride in building relationships with students early in their high school experience to assist them in discovering STEM careers. Kelly stated, “We definitely talk about it when students come to our offices. When we meet with our eighth graders coming into high school, we definitely let them know, here are your options.”
A method of bridging the gap for underrepresented students is by providing access to academic and postsecondary STEM opportunities. Christy spoke to her experience of supporting underrepresented students by providing that access:
We introduced that summer bridge class for the students. So, this will be the first year that we will potentially see the benefit of that. And hopefully seeing stronger grades in those students, especially students coming from public schools, minority students who are just now having access to the private school resources.
Similarly, Jane found value in encouraging her underrepresented students with passions in STEM to take advantage of all opportunities. Jane spoke of an encounter with a previous student. She recalled, “Last year I had a Black female student who said that she had started coding classes in middle school. . . . She really liked it, so I was like, ‘Great. We’re going to do all of them.’” In increasing access for students, the participants were intentional to ensure underrepresented students have opportunities. Kate stated, “I keep a lookout for virtual fly-in opportunities, especially when I know I have a student that’s interested in STEM and they are of a minority group, I always nominate them for those fly-ins.”
Jane summarized her role in supporting underrepresented students’ interests in STEM by saying:
“The school counselor has a huge role in not only exposing students to the possibilities of STEM careers but really targeting and explicitly encouraging Black students, Latino students to participate in and learn more about the STEM field.”
Further, regarding taking an active role in encouraging underrepresented students to pursue STEM, one participant, Kate, reflected on how her own racial identity motivates her to encourage students of color:
Me being a woman of color, I can’t help but feel like I’m rooting for everybody Black. . . . That’s not to say that I don’t encourage my non-students of color to also pursue STEM. . . . I feel like I have to really look out for my students of color, in my counseling department, I’m the only Black counselor. So, I do feel more pressure to really look out for them because I know, prior to me getting there, they weren’t inviting Historical Black Colleges and Universities [HBCUs] to come out. There was no HBCU session at our college fairs and so forth. No one was sending out information about the multicultural fly-ins. . . . Now I’m doing it and I forward it to my coworkers.
Lauren discussed how she actively identifies underrepresented students for STEM-related opportunities. Communication is key, she said: “Good communication with my teachers, so of course, math and science teachers, if they’re in tune with their students, that’s really helpful, identify the students and let me know.” In addition to communication with teachers, Lauren found value in using college and career cluster surveys with students. Lauren said the most impact her role has with students with regard to STEM is during career assessments “when they’re identifying that their talents or their personality matches up with any of the STEM fields.” She noted, “I think that’s brought in the most numbers of kids.” Other participants also used more formal career development tools. Christy stated, “We use Naviance at our school for college planning,” and Jo stated, “Our school uses Xello. It does a lot of interest surveys and gets students to see where they’re at, their personality, their interests and then matches it to careers.”
Theme 4: Barriers
Barriers related to supporting underrepresented students’ STEM interests emerged as the fourth theme, with participants reflecting on hindrances to their ability to support underrepresented students’ STEM careers and opportunities. These barriers included: COVID-19, school, administration, students’ self-efficacy, and language.
COVID-19
COVID-19 is a barrier that was presented in most of the participants’ interviews (n = 8). It was primarily identified as a context impacting students negatively and also one that resulted in changes to school counselors’ roles and day-to-day practice. When reflecting on the beginning of the pandemic, Lauren expressed, “All I did from March through May was call, email, and bother parents and seniors about graduation and making sure they were alive. That completely impacted my role for minority students pursuing STEM. . . . We were down to basic needs.” Christy also reflected on COVID-19 and said, “It’s really been bad. I would say that minorities in general, that’s probably the hardest group to get to virtually” with regard to communicating with students as a result of virtual schooling. Jo echoed Christy’s sentiments and stated, “I think the biggest challenge has been the distance, like not being able to meet them one-on-one.” Jo further explained, “Some of our students do not have all the technology they need, so they can’t jump on a Zoom, or maybe they do and the Wi-Fi is really bad.”
School
Participants also highlighted requirements at the school level that hinder students from accessing STEM careers and opportunities. Jo stated, “A student could do everything they need to graduate high school but not necessarily be ready for the university.” Jo was referring to the lack of college readiness and opportunity his school provides. Moreover, Kelly stated, “So they’re interested in that…the medical or the engineering. But when they find out, ‘I can get more credit in an AP,’ it kind of turns them off a little bit.” AP courses can help students with a weighted GPA, bring students closer to meeting graduation requirements, and give them college credits. In Kelly’s experience, her students are interested in STEM fields; however, it is hard to combat the course credit hours linked to an AP course versus a STEM course. Furthermore, in relation to school barriers, Kate mentioned the importance of anti-racist school practices:
I would probably even go as far as to say, knowing that all of our STEM teachers and faculty are anti-racist and I don’t know that all of them are. And the reason why I think that that’s important is because it’s possible that they receive opportunities for students, and are they aggressively sending or communicating those opportunities out to students of color?
Administration
In addition to COVID-19 and school barriers, participants also highlighted the lack of time and some administrative issues as barriers to supporting underrepresented students who are interested in STEM. For example, Jane discussed that high school is late in a student’s educational experience to only just begin discussing STEM:
I think the primary barrier is getting them so late. I mean, high school is late. It’s not too late, of course. It’s never too late. Students can always find their interest and their passion. But it’s not like the super early stages.
Jane further emphasized that by the time students of color are in high school, they may already lack the necessary exposure to STEM coursework:
I don’t know if any of my Black students are coming into ninth grade with that previous exposure. . . . I know that some of them are not. And so, I think that is a huge barrier. Not having them already exposed to a lot of what the STEM fields can offer.
Another challenge that participants highlighted was not having enough time to meet with students individually because of their caseload or administrative tasks. For example, Christy mentioned, “Another barrier is just time. Even with my caseload this year, I have 350 students.” Similarly, Lauren discussed “the lack of time, and the bulk of so many other responsibilities being given to counselors by administrators” as an impediment.
She further explained that the wide list of administrative duties at the high school level not only impeded her ability to meet students’ needs but also prompted her to leave high school and work at the elementary school level. Likewise, Kelly also explained how administrative tasks hinder her ability to have “meaningful conversations in a smaller school setting” because instead of meeting with students individually, she highlighted that she has “19 other things to do . . . because of the makeup of my job.”
Students’ Self-Efficacy
Participants also identified barriers regarding underrepresented students’ beliefs about STEM and their STEM abilities. Mark explained that one of the biggest issues he faces in supporting students from diverse backgrounds who are interested in STEM “is that they struggle with some of the challenging courses.” Similarly, Jane expressed that students may have struggled in STEM coursework during elementary and middle school, resulting in negative self-efficacy beliefs like “I’m not a math person or I’m not good at math.” In a similar vein, Jo explained that some of his underrepresented students do have the academic foundation; however, they “sometimes don’t feel as confident” about their STEM abilities. He stated, “I think a lot of my students, when they’re looking at these careers, sometimes they don’t see themselves in those careers and so that steers them away. . . . They just don’t feel it’s a possibility.”
Language
Lastly, some participants recognized the prevalence of barriers specific to the Latinx community. Tina mentioned the role of a counselor when helping students make the connections to various career options:
Working with Latinx and some undocumented or DACA students, the students of color, and even first-generation students . . . our role is very influential. In certain situations, especially for my kiddos whose parents don’t speak English, we are the adult, we are the person that’s helping them make those important decisions.
Some families Jo worked with did not always understand the materials about a STEM opportunity because of language barriers. He emphasized the importance of having materials in languages all families can understand:
We can sometimes talk about opportunities, but if it’s not getting into the hands of the families and if they’re not understanding what the opportunity is, they may not be as willing to allow their kid to attend maybe a 6-week program or a college program.
Discussion
STEM fields are growing in demand and are in need of talented and diverse individuals from varying gender identities and racial backgrounds (BLS, 2020; NCES, 2019). High school is the last opportunity in the K–12 system to promote and increase the pipeline of underrepresented students pursuing STEM careers. This study sought to support and extend the literature on the role of school counselors in supporting underrepresented students’ STEM career interests while also exploring the impact of context, including the COVID-19 pandemic, on STEM counseling. The findings emphasize the importance of high school counselors in promoting, encouraging, and supporting girls, racial minorities, and students at the intersections of both identities who are interested in STEM careers.
The results of this study aligned with the findings of Shillingford and colleagues (2017) that knowledge and training related to STEM professions was lacking for school counselors. Similarly, in the present study, some participants were able to identify concrete formal and informal training that they received in regard to STEM careers and diversity issues, but many of the participants in this study stated that they either received no training or were in need of more information and training related to STEM careers and diversity concerns. Further, time was similarly identified as a barrier. In both studies, school counselors explained that there is not enough time in the day to dedicate to discussing STEM career pathways with students individually.
Our findings have added a more nuanced understanding of time as a barrier for students and school counselors given its emphasis on high school. School counselors (n = 3) discussed how lack of prior STEM academic experiences can have negative consequences for high school students’ interest in STEM. For example, if a student is missing the foundational academic understanding of STEM before they get to high school, then they can fall further behind in the academic work even though they may express an interest in STEM careers. In addition, although high school is not too late to intervene and support students’ STEM interests, it is late in the academic journey to both (a) supplement academic understanding and (b) combat the internalized beliefs that students may have because of their prior educational experiences with STEM.
Similar to the work of Falco and Summers (2019), the importance of self-efficacy was explained by the participants in this study. For example, both Jo and Jane explained how Black and Latinx girls may lack confidence in themselves and not see themselves as being capable of pursuing and excelling in STEM careers. In interviews, they both observed how students either struggling in STEM coursework previously or not seeing themselves represented in STEM careers experienced diminished self-confidence regarding STEM. Although none of the participants explicitly discussed the term self-efficacy, they explained that Black and Brown students and girls may have low STEM-related self-efficacy and school counselors can play a role in increasing students’ exposure to STEM. The role high school counselors play in exposing students to diversity in STEM and diverse STEM careers is integral to challenging students’ distorted STEM self-efficacy beliefs. Moreover, Christy discussed her role in supporting students with STEM bridge courses—school counselors’ participation in these programs can help students develop STEM skills and self-efficacy.
Furthermore, in alignment with ASCA’s (2021) emphasis on school counselors’ role in supporting the social-emotional learning and career development of students, the findings in this study also revealed the importance of career development assessments in high school counselors’ ability to support students. Career assessment tools and platforms such as Naviance, Xello, CollegeBoard, etc., provided participants in this study with the tools to 1) identify students who may be interested in STEM careers and 2) help students connect their interests and abilities to STEM careers. Though school counselors might be pressed for time, utilizing career assessments can help structure individual meetings with students and open the door to follow-up conversations and programming surrounding careers in STEM.
In addition, the findings also revealed the importance of making community connections and utilizing social media to further support underrepresented students as they pursue STEM careers. Participants mentioned the importance of connecting students with HBCUs or other colleges in the area in order to help underrepresented students explore postsecondary options in STEM. Moreover, to increase students’ access to representation, as Dawn mentioned, high school counselors can expose students to social media campaigns that emphasize the representation of Black women in STEM, Latinx women in STEM, Native American men in STEM, and more. Increasing students’ access to more diverse images and professionals in STEM can help students to think about what being in STEM can look like after high school and, therefore, begin to see themselves in those STEM positions.
With the current emphasis on anti-racist educational processes in mind, the findings revealed the importance of communication. Participants explained that specifically, communication with math and science teachers is critical to identifying and supporting underrepresented students who are exhibiting strong potential in STEM. Additionally, Kate pointed out the importance of knowing that everyone in the school, including teachers and school counselors, are engaging in anti-racist practices in order to communicate with underrepresented students surrounding opportunities that increase access to STEM. Schmidt and colleagues (2012) also emphasized the importance of school counselors encouraging teachers to remove systemic barriers to students’ educational success. Moreover, Jo and Tina highlighted the importance of having materials for students and parents in various languages in order to communicate STEM possibilities. In engaging in anti-racist practices, it is important for school counselors to collaborate with school administrators to reduce barriers in communication, particularly surrounding the languages used to share STEM opportunities targeted to underrepresented students.
Overall, the findings of this study revealed that COVID-19 has resulted in additional barriers to supporting underrepresented high school students’ STEM career interests. In alignment with the emerging literature surrounding COVID-19 and its impact on the educational system, participants explained the technology gap is even wider for their Black and Brown students (Aguilar, 2020). Students’ inadequate access to technology has made it difficult for school counselors even to check in with students, much less discuss students’ STEM career aspirations. As Lauren mentioned, many school counselors have been addressing students’ basic needs during the pandemic. Although many STEM companies are still hiring during the pandemic and STEM careers are still projected to grow even after the pandemic, school counselors’ conversations with underrepresented students regarding STEM may be stalled at this time.
Implications
The present study has implications for school counseling practice, counselor education, and school administration. As expressed in the participants’ interviews, high school counselors care deeply about supporting underrepresented students’ STEM interests, despite the barriers. At the same time, high school counselors may be limited in their own training and their knowledge of STEM opportunities. Furthermore, COVID-19 has resulted in additional barriers for school counselors who may already be confronted with limited time and resources.
School Counseling
Students may benefit from school counselors sharing more STEM postsecondary options. For example, when discussing postsecondary options related to STEM, none of the participants discussed students participating in apprenticeships. Most participants reflected on connecting students to universities, including HBCUs. However, apprenticeships are paid industry-driven experiences in which students can receive specialized training with a company (U.S. Department of Labor, n.d.). Many apprenticeship programs are related to STEM. For example, there are apprenticeships for information technology specialists, medical laboratory specialists, and pharmacy technicians. In addition, a main benefit of completing an apprenticeship program in a STEM industry after high school is that after the completion of their apprenticeship, over 90% of employers retain their apprentices for full-time employment.
Moreover, although COVID-19 has shifted many schools to virtual formats, there are still opportunities for school counselors to help underrepresented students. For example, many STEM companies, such as Boeing, AT&T, Abbott, and more, are offering students virtual internship experiences. Websites such as Vault.com have offered virtual internship job search tools during the pandemic. In addition, online tools such as LinkedIn Learning can provide students ages 16 and above with access to training opportunities related to coding, math, and science concepts. School counselors increasing their knowledge about practical virtual STEM resources can help increase underrepresented students’ access to STEM careers during the pandemic. Through connecting with local university and community college career services departments, school counselors can learn more about STEM resources to share with students. In addition, there are several STEM-focused social media groups that school counselors can join in order to learn more about STEM. School counselors with an interest in STEM can develop more state or regional interest networks within their school counseling organizations in order to share resources and information with each other.
Counselor Education
This study also has several implications for counselor educators who will train the next generation of school counselors. Several participants highlighted that they had limited or no training on STEM career opportunities. In order to help increase school counselors’ knowledge regarding the need for STEM professionals and the ways that they can support underrepresented students, counselor educators can incorporate this learning into career counseling coursework. For instance, as an assignment, counselor educators can help school counseling graduate students utilize career counseling theory to develop a program aimed at promoting STEM to underrepresented high school students. Utilizing career counseling coursework to encourage students to find creative solutions to career-related issues can help make this course more meaningful and practically significant for future school counselors.
In addition, counselor educators can engage in research endeavors to build the literature connecting school counseling and STEM education. In doing so, counselor educators can host webinars, present at conferences, and disseminate information in both school counseling newsletters and professional journals in order to help increase school counselors’ knowledge on the needs of underrepresented students who may be interested in STEM. Additionally, counselor educators can collaborate with ASCA to conduct professional development opportunities for school counselors that explain relevant literature on STEM and how school counselors help develop students’ STEM career aspirations.
School Administration
Similarly, school administrators can support and encourage school counselors to attend professional development opportunities regarding STEM. This support can entail sharing STEM-related professional development opportunities with school counselors and giving school counselors the time to attend these professional development opportunities. Additionally, school administrators could benefit from listening to school counselors’ recommendations for how schools can better support underrepresented students and ensure equitable access to STEM coursework. Further, school administrators can review policies to incorporate anti-racist practices that promote STEM to diverse populations of students. These practices can include: (a) reviewing the racial and gender makeup of STEM courses to ensure equitable representation of students in STEM courses; (b) building connections with community organizations and stakeholders that provide resources to underrepresented students who are interested in STEM; and (c) ensuring that school counselors have access to documents regarding STEM opportunities to share with students and their parents in multiple languages, including both English and Spanish. Moreover, school administrators can work to ensure that the duties assigned to school counselors align with the ASCA National Model (2012) and allow school counselors to focus on STEM-related career development interventions for students.
Limitations and Future Research
There are several limitations to this study that warrant discussion. First, many of the participants in this study were counselors of color. Thus, there may be an element of self-selection bias wherein participants (school counselors of color) were more inclined to value the purpose of the study and be more connected to the experiences of underrepresented students. Hence, future research can emphasize the importance of all school counselors, regardless of race, addressing the needs of underrepresented students in STEM. Similarly, all the counselors in this study were several years removed from their graduate school experience. School counselors who have graduated recently may have more training and awareness of the disparities in STEM; thus, future studies can explore beginning counselors’ knowledge of STEM issues and support of underrepresented students.
In addition, all interviews were conducted virtually, which can increase the likelihood of response inhibition, wherein participants were uncomfortable with confidentiality and privacy when speaking across the internet (Janghorban et al., 2014). Future studies that are not limited by a pandemic or geography may benefit from doing in-person interviews in participants’ schools or an environment where the participants feel more comfortable. Although validity practices such as journaling, external auditing, and check-ins were utilized by our lead researcher, her closeness to the topic as both a professional and a Black woman may have impacted the objectivity of the study. The sample size was in accordance with phenomenological research; however, an increased sample size that is even more representative of school counselors from high schools across the nation could help increase this study’s generalizability.
Future research studies can explore the educational experiences of underrepresented professionals (e.g., Black women) in STEM in order to better understand what makes students pursue and stay in STEM fields as well as the role of the school counselor in their future success in STEM. In addition, future studies can explore how school counselors can collaborate with career advisors at local colleges in order to increase diversity in the STEM pipeline. In a similar vein, future studies can explore the experiences of underrepresented high school students who received STEM-related support from their school counselors and transitioned to college to pursue a major in STEM. Also, very few of the participants in this study explicitly spoke to their experience supporting Native American and Indigenous students. Given the lack of Indigenous and Native American professionals in STEM, future studies can specifically focus on their needs with regard to STEM education.
Conclusion
In sum, school counselors play a vital role in supporting the academic and career success of all students. For students who may find themselves underrepresented in STEM, high school counselors can make the difference by exposing them to possibilities and opportunities in STEM. High school might be some students’ last opportunity to (a) explore and discover varying career paths, (b) complete the preparation needed for a smooth transition to college, and/or (c) access resources to support diversity in STEM. In spite of barriers and limitations, school counselors ensure that students, regardless of gender or race, do not fall through the cracks and are encouraged to pursue any profession they desire, including a career in STEM.
Conflict of Interest and Funding Disclosure
This study was made possible by a grant from
the Virginia Counseling Association Foundation.
The authors reported no conflict of interest
for the development of this manuscript.
References
Aguilar, S. J. (2020). Guidelines and tools for promoting digital equity. Information and Learning Sciences, 121(5/6), 285–299. https://doi.org/10.1108/ILS-04-2020-0084
American School Counselor Association. (2012). ASCA national model: A framework for school counseling programs (3rd ed.).
American School Counselor Association. (2021). School counseling and school reentry during COVID-19. https://schoolcounselor.org/Publications-Research/Publications/Free-ASCA-Resources/COVID-19-Resources
Cataldi, E. F., Siegel, P., Shepherd, B., & Cooney, J. (2014). Baccalaureate and beyond: A first look at the employment experiences and lives of college graduates, 4 Years On (B&B:08/12) (NCES 2014-141). National Center for Education Statistics, Institute of Education Sciences, U.S. Department of Education. https://nces.ed.gov/pubs2014/2014141.pdf
Chen, X. (2013). STEM attrition: College students’ paths into and out of STEM fields (NCES 2014-001). National Center for Education Statistics, Institute of Education Sciences, U.S. Department of Education. https://nces.ed.gov/pubs2014/2014001rev.pdf
Creswell, J. W., & Poth, C. N. (2017). Qualitative inquiry & research design: Choosing among five approaches (4th ed.). SAGE.
Curry, J. R., & Shillingford, M. A. (2015). African American students’ career college readiness: The journey unraveled. Lexington Books.
Dockery, D. J., & McKelvey, S. (2013). Underrepresented college students’ experiences with school counselors. Journal of School Counseling, 11(3), n3. https://files.eric.ed.gov/fulltext/EJ1012298.pdf
Falco, L. D. (2017). The school counselor and STEM career development. Journal of Career Development, 44(4), 359–374. https://doi.org/10.1177/0894845316656445
Falco, L. D., & Summers, J. J. (2019). Improving career decision self-efficacy and STEM self-efficacy in high school girls: Evaluation of an intervention. Journal of Career Development, 46(1), 62–76.
https://doi.org/10.1177/0894845317721651
Funk, C., & Parker, K. (2018). Diversity in the STEM workforce varies widely across jobs. Pew Research Center.
https://www.pewsocialtrends.org/2018/01/09/diversity-in-the-stem-workforce-varies-widely-across-jobs
Grossman, J. M., & Porche, M. V. (2014). Perceived gender and racial/ethnic barriers to STEM success. Urban Education, 49(6), 698–727. https://doi.org/10.1177%2F0042085913481364
Hamilton, A. F., Malin, J., & Hackmann, D. (2015). Racial/ethnic and gender equity patterns in Illinois high school career and technical education coursework. Journal of Career and Technical Education, 30(1), 29–52.
https://doi.org/10.21061/jcte.v30i1.712
Janghorban, R., Latifnejad Roudsari, R., & Taghipour, A. (2014). Skype interviewing: The new generation of online synchronous interview in qualitative research. International Journal of Qualitative Studies on Health and Well-Being, 9(1), 24152. https://doi.org/10.3402/qhw.v9.24152
Mau, W.-C. J. (2016). Characteristics of US students that pursued a STEM major and factors that predicted their persistence in degree completion. Universal Journal of Educational Research, 4(6), 1495–1500.
https://doi.org/10.13189/ujer.2016.040630
Mau, W.-C. J., & Li, J. (2018). Factors influencing STEM career aspirations of underrepresented high school students. The Career Development Quarterly, 66(3), 246–258. https://doi.org/10.1002/cdq.12146
Maxwell, J. A. (2005). Qualitative research design: An interactive approach (2nd ed.). SAGE.
Moustakas, C. (1994). Phenomenological research methods. SAGE.
National Center for Education Statistics. (2019). Status and trends in the education of racial and ethnic groups.
https://nces.ed.gov/programs/raceindicators/indicator_reg.asp
National Center for Education Statistics. (2020). High School Longitudinal Study of 2009 (HSLS:09). https://nces.ed.gov/surveys/hsls09/hsls09_data.asp
National Science Foundation. (2019). Women, minorities, and persons with disabilities in science and engineering: 2019. National Center for Science and Engineering Statistics Special Report NSF 19–304. https://www.nsf.gov/statistics/wmpd
National Science and Technology Council. (2018). Charting a course for success: America’s strategy for STEM education. Office of Science and Technology Policy. https://www.energy.gov/sites/prod/files/2019/05/f62/STEM-Education-Strategic-Plan-2018.pdf
Savitz-Romer, M., Rowan-Kenyon, H. T., Nicola, T. P., Carroll, S., & Hecht, L. (2020). Expanding support beyond the virtual classroom: Lessons and recommendations from school counselors during the COVID-19 crisis. Harvard Graduate School of Education & Boston College Lynch School of Education and Human Development. https://www.gse.harvard.edu/sites/default/files/documents/School-Counseling-Covid-19-Report.pdf
Schmidt, C. D., Hardinge, G. B., & Rokutani, L. (2012). Expanding the school counselor repertoire through STEM-focused career development. The Career Development Quarterly, 60(1), 25–35.
https://doi.org/10.1002/j.2161-0045.2012.00003.x
Shillingford, M. A., Oh, S., & Finnell, L. R. (2017). Promoting STEM career development among students and parents of color. Professional School Counseling, 21(1b), 1–11. https://doi.org/10.1177/2156759X18773599
U.S. Bureau of Labor Statistics. (2020). Employment projections: Employment in STEM occupations. https://www.bls.gov/emp/tables/stem-employment.htm
U.S. Department of Education. (n.d.). Science, technology, engineering, and math, including computer science.
https://www.ed.gov/stem
U.S. Department of Labor. (n.d.). Discover apprenticeship: Earn while you learn today. https://www.apprenticeship.gov/sites/default/files/Career_Seeker_Fact_Sheet.pdf
Vilorio, D. (2014). STEM 101: Intro to tomorrow’s jobs. https://www.bls.gov/careeroutlook/2014/spring/art01.pdf
Xue, Y., & Larson, R. C. (2015). STEM crisis or STEM surplus? Yes and yes. https://www.bls.gov/opub/mlr/2015/article/stem-crisis-or-stem-surplus-yes-and-yes.htm
Appendix
Interview Questions
What is your understanding of the issues of diversity in STEM?
What training did you receive regarding the needs of underrepresented students who are interested in STEM?
What do you believe is the role of a school counselor in supporting underrepresented students’ interest in STEM careers?
What is your role in supporting STEM academic and career opportunities for underrepresented students?
What has been your experience in promoting STEM careers to underrepresented students?
How do you identify underrepresented students who may have potential or interest in STEM careers?
What barriers do you face in promoting STEM careers to underrepresented students?
What school and community factors influence your ability to support underrepresented students’ STEM career aspirations and interests?
How do you prepare underrepresented students for postsecondary opportunities in STEM?
What do you wish was different about how you support underrepresented students’ STEM career interests and aspirations?
How has the COVID-19 pandemic impacted your role in supporting underrepresented students’ STEM career aspirations and interests?
The authors would like to thank and acknowledge the Virginia Counseling Association Foundation; and Lexi Caliendo and Kirsten Nozime for their feedback, which improved the quality of this study. Autumn L. Cabell, PhD, NCC, LPC, CCC, CCTP, is an assistant professor at DePaul University. Dana Brookover, PhD, NCC, is an assistant professor at the University of Scranton. Amber Livingston, MEd, is a doctoral student at Virginia Commonwealth University. Ila Cartwright, MEd, is a doctoral student at Virginia Commonwealth University. Correspondence may be addressed to Autumn L. Cabell, DePaul University, 2247 N Halsted St., Rm. 246, Chicago, IL 60614, acabell@depaul.edu.
Sep 27, 2018 | Volume 8 - Issue 3
Christopher T. Belser, M. Ann Shillingford, Andrew P. Daire, Diandra J. Prescod, Melissa A. Dagley
The United States is facing a crisis with respect to filling job vacancies within science, technology, engineering, and math (STEM) industries and with students completing STEM undergraduate degrees. In addition, disparities exist for females and ethnic minorities within STEM fields. Whereas prior research has centered on disparities in STEM fields, retention rates, and some intervention programs, researchers have not given much attention to the role of career development initiatives within STEM recruitment and retention programming. The purpose of the present study was to incorporate demographic variables, math performance, and career development–related factors into predictive models of STEM retention with a sample of undergraduate students within a STEM recruitment and retention program. The resulting two models accurately predicted first-year to second-year retention with 73.4% of the cases and accurately predicted first-year to third-year retention with 70.0% of the cases. Based on the results, the researchers provide a rationale for STEM career programming in K–12 and higher education settings and for the inclusion of career development and career counseling in STEM education programming.
Keywords: STEM, retention, career development, career counseling, undergraduate student
The United States lacks an adequate number of workers to keep up with the demand for trained workers in science, technology, engineering, and mathematics (STEM) fields (National Center for Science and Engineering Statistics [NCSES], 2017; National Science Board, 2018; Sithole et al., 2017). Researchers have pointed to the overall stagnancy of undergraduate students declaring and completing STEM degrees (Carnevale, Smith, & Melton, 2011; Doerschuk et al., 2016; Sithole et al., 2017). Additionally, underrepresentation is a problem for racial and ethnic minorities and females in STEM fields (NCSES, 2017). Because of these disparities, universities have developed programs centered on recruitment and retention of STEM undergraduates (Bouwma-Gearhart, Perry, & Presley, 2014; Dagley et al., 2016; Schneider, Bickel, & Morrison-Shetlar, 2015) and both government and private entities invest billions of dollars annually toward STEM initiatives at the K–12 and higher education levels (Carnevale et al., 2011). However, many of these endeavors have failed to incorporate components centered on career development or career planning.
The National Career Development Association (2015) defined career development as “the sequence of career-related choices and transitions made over the life span” (p. 4) and career planning as a structured process through which a person makes decisions and plans for a future career. Career development activities, such as structured career planning courses, have shown efficacy with general undergraduate populations (Osborn, Howard, & Leierer, 2007; Reardon, Melvin, McClain, Peterson, & Bowman, 2015) but have been studied less commonly with STEM-specific undergraduate populations (Belser, Prescod, Daire, Dagley, & Young, 2017, 2018; Prescod, Daire, Young, Dagley, & Georgiopoulos, in press). In the present study, researchers examined a STEM recruitment and retention program that did include a career planning course. More specifically, the research team sought to investigate relationships between demographics (e.g., gender, ethnicity), math scores, and various aspects of the undergraduate STEM program and student retention in the first 2 years of college.
Gender, Ethnicity, and STEM
Gender disparities are a common sight within STEM degree programs and the larger STEM workforce (NCSES, 2017). Females who are interested in math and science are more likely to be tracked into non-diagnosing health practitioner fields, such as nursing (ACT, 2018; NCSES, 2017). Some researchers have pointed to the K–12 arena as the root of these gender disparities that permeate undergraduate programs and STEM professions (Mansfield, Welton, & Grogan, 2014), whereas others have identified specific problems, such as differences in math and science course completion over time (Chen & Soldner, 2013; Riegle-Crumb, King, Grodsky, & Muller, 2012), stereotype threat (Beasley & Fischer, 2012), and STEM confidence (Litzler, Samuelson, & Lorah, 2014). As a result, existing predictive models typically indicate a lower likelihood of females completing a STEM degree compared to male students (Cundiff, Vescio, Loken, & Lo, 2013; Gayles & Ampaw, 2014).
Similarly, disparities in STEM degree completion and STEM job attainment exist between ethnic groups (NCSES, 2017; Palmer, Maramba, & Dancy, 2011). Although progress has been made in degree attainment in certain STEM areas, other areas have stagnated or are declining in participation by ethnic minority students (Chen & Soldner, 2013; NCSES, 2017). Foltz, Gannon, and Kirschmann (2014) identified protective factors for minority students in STEM, such as receiving college-going expectations from home, establishing connections with STEM faculty members (particularly those of color), and developing connections with other minority students in STEM majors; however, the disparities in STEM programs help perpetuate a cycle of many students not being exposed to these protective factors. The intersectionality of ethnicity and gender in STEM fields has become a topic producing interesting findings (Riegle-Crumb & King, 2010). In addition to observing disparities across ethnic groups, researchers have observed disparities within ethnic groups based on gender (Beasley & Fischer, 2012; Cundiff et al., 2013; Riegle-Crumb & King, 2010). Specifically with males of color, predictive models have been inconclusive, with some showing a higher likelihood of completing a STEM degree (Riegle-Crumb & King, 2010) and others showing a lower likelihood (Cundiff et al., 2013; Gayles & Ampaw, 2014).
Mathematics and STEM
The SAT is one of the most widely used college admissions tests (CollegeBoard, 2018). Researchers have correlated the math sub-score with undergraduate math and science classes within the first year, indicating that higher SAT math scores indicate a higher probability of higher course grades in math and science courses (Wyatt, Remigio, & Camara, 2012). Additionally, researchers have identified SAT scores as predictors of academic success and university retention (Crisp, Nora, & Taggart, 2009; Le, Robbins, & Westrick, 2014; Mattern & Patterson, 2013; Rohr, 2012). Despite its wide use in higher education admissions, the SAT may not be free from bias. Numerous scholars have highlighted potential test bias, particularly against ethnic minorities (Dixon-Román, Everson, & McArdle, 2013; Lawlor, Richman, & Richman, 1997; Toldson & McGee, 2014). Nevertheless, its wide use makes it a prime instrument for research.
In addition to the SAT scores, researchers also have demonstrated that taking higher-level math courses and having higher math self-efficacy translate to better outcomes within STEM majors (Carnevale et al., 2011; Chen & Soldner, 2013; Nosek & Smyth, 2011). Specifically, taking calculus-based courses in high school correlated with retention in STEM majors (Chen & Soldner, 2013). Nosek and Smyth (2011) found connections between gender and internalized math variables, such as warmth for math, identification with math, and self-efficacy; females across the life span showed lower levels of each of these variables, but the authors did not test these against retention outcomes in STEM majors. However, one could hypothesize that having lower levels of warmth toward math and not being able to identify with math would likely impact one’s career decisions, particularly related to math and science fields.
Career Interventions and STEM
Career theory can provide for understanding one’s interest in STEM fields (Holland, 1973), one’s exposure to STEM fields (Gottfredson, 1981), and one’s beliefs or expectations about the process of choosing a STEM field (Lent, Brown, & Hackett, 2002; Peterson, Sampson, Lenz, & Reardon, 2002). However, career interventions, such as a career planning class, are more likely to make a direct impact on career outcomes with undergraduates. In one review of research on undergraduate career planning courses, more than 90% of the courses produced some measurable positive result for students, such as increased likelihood of completing a major, decreased negative career thinking, and increased career self-efficacy (Reardon & Fiore, 2014). Other researchers have reported similar results with generic undergraduate career planning courses (Osborn et al., 2007; Saunders, Peterson, Sampson, & Reardon, 2000).
Researchers have studied structured career planning courses specific to STEM majors with much less frequency. In one such study, Prescod and colleagues (in press) found that students who took a STEM-focused career planning course scored lower on a measure of negative career thinking at the end of the semester. In a similar study, STEM-interested students in a STEM-focused career planning course had lower posttest scores on a measure of negative career thinking than declared STEM majors at the end of the same semester (Belser et al., 2018). Additionally, in a pilot study, Belser and colleagues (2017) found that greater reductions in negative career thinking predicted higher odds of being retained in a STEM major from the first to second year of college; in this same study, the authors found that students who participated in a STEM-focused career planning course were more likely to be retained in a STEM major than students in an alternative STEM course. Researchers have not given ample attention to determining how career planning and other career variables fit into predictive models of retention in STEM majors.
Statement of the Problem and Hypotheses
As previously noted, prior researchers have paid limited attention to developing predictive models that incorporate career development variables along with demographics and math performance. Developing effective predictive models has implications for researchers, career practitioners, higher education professionals, and the STEM workforce. To this end, the researchers intend to test two such models related to retention in STEM majors using the following hypotheses:
Hypothesis 1: First-year to second-year undergraduate retention in STEM majors can be predicted by ethnicity, gender, initial major, math placement–algebra scores, SAT math scores, STEM course participation, and Career Thoughts Inventory (CTI) change scores.
Hypothesis 2: First-year to third-year undergraduate retention in STEM majors can be predicted by ethnicity, gender, initial major, math placement–algebra scores, SAT math scores, STEM course participation, and CTI change scores.
Methods
In this study, researchers examined multi-year retention data for students in a STEM recruitment and retention program at a large research university in the Southeastern United States and utilized a quasi-experimental design with non-equivalent comparison groups (Campbell & Stanley, 1963; Gall, Gall, & Borg, 2007). Because this study was part of a larger research project, Institutional Review Board approval was already in place.
The COMPASS Program
The COMPASS Program (Convincing Outstanding Math-Potential Admits to Succeed in STEM; Dagley et al., 2016) is a National Science Foundation–funded project that seeks to recruit and retain undergraduate students in STEM majors. To enter the program, students must have a minimum SAT math score of 550, an undeclared major at the time of applying to the university and program, and an expressed interest in potentially pursuing a STEM degree. However, some students accepted to the COMPASS Program declare a STEM major between the time that they are accepted into the COMPASS Program and the first day of class, creating a second track of students who were initially uncommitted to a major at the time of application. Students in both tracks have access to math and science tutoring in a program-specific center on campus, are matched with undergraduate mentors from STEM majors, have access to cohort math classes for students within the program, and can choose to live in a residence hall area designated for COMPASS participants. Depending on which COMPASS track students are in, they either take a STEM-focused career planning course or a STEM seminar course during their first semester.
COMPASS participants who started college without a declared major take a STEM-focused career planning class in their first semester. The activities of this course include a battery of career assessments and opportunities to hear career presentations from STEM professionals, visit STEM research labs, and attend structured career planning activities (e.g., developing a career action plan, résumé and cover letter writing, small group discussions). The first author and fourth author served as instructors for this course, and both were counselor education doctoral students at the time.
Participants who had declared a STEM major between the time they were accepted into the COMPASS Program and the first day of class took a STEM seminar course instead of the career planning class. The structure of this course included activities designed to help students engage with and be successful in their selected STEM majors, including presentations on learning styles and strategies, time management, study skills, professional experiences appropriate for STEM majors, and strategies for engaging in undergraduate research. Guest speakers for the class focused more on providing students with information about how to be successful as a STEM student. The course did not include career planning or career decision-making activities specifically geared toward helping students decide on a major or career field. A science education doctoral student served as the instructor of record for the course, with graduate students from various STEM fields serving as teaching assistants.
Participants
The university’s Institutional Knowledge Management Office provided demographic data on program participants. Table 1 displays descriptive data for participants, organized by second-year retention data (i.e., retention from the first year of college to the second year of college, for Hypothesis 1) and third-year retention data (i.e., retention from the first year of college to the third year of college, for Hypothesis 2). The frequencies for the subcategories were smaller for the third-year retention data (Hypothesis 2) because fewer participants had matriculated this far during the life of the project. Table 1 also breaks down each subset of the data based on which students were retained in a STEM major and which were not retained.
Table 1
Descriptive Statistics for Categorical Variables
|
Second-Year Retention Descriptives |
Third-Year Retention Descriptives |
| Variables |
Retained |
Not Retained |
Total |
Retained |
Not Retained |
Total |
|
n |
%a |
n |
%b |
n |
%c |
n |
%a |
n |
%b |
n |
%c |
| Gender |
|
|
|
|
|
|
|
|
|
|
|
|
| Male |
159 |
58.9 |
74 |
46.5 |
233 |
54.3 |
72 |
55.8 |
65 |
44.8 |
137 |
50.0 |
| Female |
111 |
41.1 |
85 |
53.5 |
196 |
45.7 |
57 |
44.2 |
80 |
55.2 |
137 |
50.0 |
| Total |
270 |
100.0 |
159 |
100.0 |
429 |
100.0 |
129 |
100.0 |
145 |
100.0 |
274 |
100.0 |
| Ethnicity |
|
|
|
|
|
|
|
|
|
|
|
|
| Caucasian/White |
147 |
54.4 |
100 |
62.9 |
247 |
57.6 |
66 |
51.2 |
85 |
58.6 |
151 |
55.1 |
| African Am./Black |
31 |
11.5 |
16 |
10.1 |
47 |
11.0 |
16 |
12.4 |
18 |
12.4 |
34 |
12.4 |
| Hispanic |
57 |
21.1 |
34 |
21.4 |
91 |
21.2 |
29 |
22.5 |
32 |
22.1 |
61 |
22.3 |
| Asian/Pacific Islander |
24 |
8.9 |
4 |
2.5 |
28 |
6.5 |
10 |
7.8 |
5 |
3.4 |
15 |
5.5 |
| Other |
11 |
4.1 |
5 |
3.1 |
16 |
3.7 |
8 |
6.2 |
5 |
3.4 |
13 |
4.7 |
| Total |
270 |
100.0 |
159 |
100.0 |
429 |
100.0 |
129 |
100.0 |
145 |
100.0 |
274 |
100.0 |
| Course |
|
|
|
|
|
|
|
|
|
|
|
|
| Career Planning |
137 |
50.7 |
120 |
75.5 |
257 |
59.9 |
76 |
58.9 |
112 |
77.2 |
188 |
68.6 |
| STEM Seminar |
133 |
49.3 |
39 |
24.5 |
172 |
40.1 |
53 |
41.1 |
33 |
22.8 |
86 |
31.4 |
| Total |
270 |
100.0 |
159 |
100.0 |
429 |
100.0 |
129 |
100.0 |
145 |
100.0 |
274 |
100.0 |
| Initial Major |
|
|
|
|
|
|
|
|
|
|
|
|
| Undeclared |
130 |
48.1 |
72 |
45.3 |
202 |
47.1 |
65 |
50.4 |
63 |
43.4 |
128 |
46.7 |
| STEM |
124 |
45.9 |
40 |
25.2 |
164 |
38.2 |
55 |
42.6 |
39 |
26.9 |
94 |
34.3 |
| Non-STEM |
16 |
5.9 |
47 |
29.6 |
63 |
14.7 |
9 |
7.0 |
43 |
29.7 |
52 |
19.0 |
| Total |
270 |
100.0 |
159 |
100.0 |
429 |
100.0 |
129 |
100.0 |
145 |
100.0 |
274 |
100.0 |
Note. a = percentage of the Retained group. b = percentage of the Not Retained group. c = percentage of the Total group.
Gender representation within the two samples was split relatively evenly, with female participants represented at a higher rate in the sample than in the larger population of STEM undergraduates and at a higher rate than STEM professionals in the workforce. Both samples were predominantly Caucasian/White, with no other ethnic group making up more than one-fourth of either sample individually; these ethnicity breakdowns were reflective of the university’s undergraduate population and somewhat reflective of STEM disciplines. The students who took the STEM-focused career planning course accounted for a larger percentage of both total samples and also of the not-retained groups. Regarding initial major, the largest percentage of students fell within the initially undeclared category, with the next largest group being the initially STEM-declared group (these students officially declared a STEM major but were uncommitted with their decision).
The researchers conducted an a priori power analysis using G*Power 3 (Cohen, 1992; Faul, Erdfelder, Lang, & Buchner, 2007), and the overall samples of 429 and 271 were sufficient for the binary logistic regression. With logistic regression, the ratio of cases in each of the dependent outcomes (retained or not retained) to the number of independent variable predictors must be sufficient (Agresti, 2013; Hosmer, Lemeshow, & Sturdivant, 2013; Tabachnick & Fidell, 2013). Following Peduzzi, Concato, Kemper, Holford, and Feinstein’s (1996) rule of 10 cases per outcome per predictor, the samples were sufficient for all independent variables except ethnicity, which had multiple categories with fewer than 10 cases. However, Field (2009) and Vittinghoff and McCulloch (2006) recommended having a minimum of five cases per outcome per predictor, which the sample achieved for all independent variables.
Variables and Instruments
The analysis included 10 independent variables within the logistic regression models. The university’s Institutional Knowledge Management Office (IKMO) provided data for the four categorical variables displayed in Table 1 (gender, ethnicity, course, and initial major). Four of the independent variables represented the participants’ total and subscale scores on the CTI, which students completed in either the career planning course or the STEM seminar course. The other two independent variables were participants’ scores on the SAT math subtest and the university’s Math Placement Test–Algebra subscale; the IKMO provided these data as well.
Career Thoughts Inventory (CTI). The CTI includes 48 Likert-type items and seeks to measure respondents’ levels of negative career thinking (Sampson, Peterson, Lenz, Reardon, & Saunders, 1996a, 1996b). To complete the CTI, respondents read the 48 statements about careers and indicate how much they agree using a 4-point scale (strongly disagree to strongly agree). The CTI provides a total score and scores for three subscales: (a) Decision Making Confusion (DMC); (b) Commitment Anxiety (CA); and (c) External Conflict (EC). Completing the instrument yields raw scores for the assessment total and each of the three subscales, and a conversion table printed on the test booklet allows respondents to convert raw scores to T scores. Higher raw scores and T scores indicate a higher level of problematic thinking in each respective area, with T scores at or above 50 indicating clinical significance. For the college student norm group, internal consistency alpha coefficients were .96 for the total score and ranged from .77 to .94 for the three subscales (Sampson et al., 1996a, 1996b). With the sample in the present study, the researchers found acceptable alpha coefficients that were comparable to the norm group. The researchers used CTI change scores as predictors, calculated as the change in CTI total and subscale scores from the beginning to the end of either the career planning class or the STEM seminar class.
SAT Math. High school students take the SAT as a college admissions test typically in their junior and/or senior years (CollegeBoard, 2018). Although the SAT has four subtests, the researchers only used the math subtest in the present study. The math subtest is comprised of 54 questions or tasks in the areas of basic mathematics knowledge, advanced mathematics knowledge, managing complexity, and modeling and insight (CollegeBoard, 2018; Ewing, Huff, Andrews, & King, 2005). In a validation study of the SAT, Ewing et al. (2005) found an internal consistency alpha coefficient of .92 for the math subtest and alpha coefficients ranging from .68 to .81 for the four math skill areas. The researchers were unable to analyze psychometric properties of the SAT math test with the study sample because the university’s IKMO only provided composite and subtest total scores, rather than individual item responses.
Math Placement Test–Algebra Subtest. The Math Placement Test is a university-made assessment designed to measure mathematic competence in algebra, trigonometry, and pre-calculus that helps the university place students in their first math course at the university. All first-time undergraduate students at the university are required to take the test; when data collection began, the mandatory completion policy was not yet in place, so some earlier participants had missing data in this area. The test is structured so that all respondents first take the algebra subtest and if they achieve 70% accuracy, they move to the trigonometry and pre-calculus subtests. Similar to the SAT, the researchers were unable to analyze psychometric properties of the test because the IKMO provided only composite and subtest total scores.
Procedure
Because the dependent variables (second-year retention and third-year retention) were dichotomous (i.e., retained or not retained), the researchers used the binary logistic regression procedure within SPSS Version 24 to analyze the data (Agresti, 2013; Hosmer et al., 2013; Tabachnick & Fidell, 2013). The purpose of binary logistic regression is to test predictors of the binary outcome by comparing the observed outcomes and the predicted outcomes first without any predictors and then with the chosen predictors (Hosmer et al., 2013). The researchers used a backward stepwise Wald approach, which enters all predictors into the model and removes the least significant predictors one by one until all of the remaining predictors fall within a specific p value range (Tabachnick & Fidell, 2013). The researchers chose to set the range as p ≤ .20 based on the recommendation of Hosmer et al. (2013).
Preliminary data analysis included identifying both univariate and multivariate outliers, which were removed from the data file; conducting a missing data analysis; and testing the statistical assumptions for logistic regression. There were no missing values for categorical variables, but the assessment variables (CTI, SAT, and Math Placement Test) did have missing values. Results from Little’s (1988) MCAR test in SPSS showed that these data were not missing completely at random (Chi-square = 839.606, df = 161, p < .001). The researchers chose to impute missing values using the Expectation Maximization procedure in SPSS (Dempster, Laird, & Rubin, 1977; Little & Rubin, 2002). The data met the statistical assumptions of binary logistic regression related to multicollinearity and linearity in the logit (Tabachnick & Fidell, 2013). As previously discussed, the data also sufficiently met the assumption regarding the ratio of cases to predictor variables, with the exception of the ethnicity variable; after removing outliers, the Asian/Pacific Islander subcategory in the non-retained outcome had only four cases, violating the Peduzzi et al. (1996) and Field (2009) recommendation of having at least five cases. However, because the goal was to test the ethnicity categories separately rather than collapsing them to fit the recommendation, and because Hosmer et al. (2013) noted this was a recommendation and not a rule, the researchers chose to keep the existing categories, noting the potential limitation when interpreting this variable.
Results
The sections that follow provide the results from each of the hypotheses and interpretation of the findings.
Hypothesis 1
Hypothesis 1 stated that the independent variables could predict undergraduate STEM retention from Year 1 to Year 2. As stated previously, the backward stepwise Wald approach involved including all predictors initially and then removing predictors one by one based on p value until all remaining predictors fell within the p ≤ .20 range. This process took five steps, resulting in the removal of four variables with p values greater than .20: (a) CTI Commitment Anxiety Change, (b) CTI External Conflict Change, (c) Gender, and (d) CTI Decision Making Confusion Change, respectively. The model yielded a Chi-square value of 91.011 (df = 10, p < .001), a -2 Log likelihood of 453.488, a Cox and Snell R-square value of .198, and a Nagelkerke R-square value of .270. These R-square values indicate that the model can explain between approximately 20% and 27% of the variance in the outcome. The model had a good fit with the data, as evidenced by the Hosmer and Lemeshow Goodness of Fit Test (Chi-square = 6.273, df = 8, p = .617). The final model accurately predicted 73.4% of cases across groups; however, the model predicted the retained students more accurately (89.6% of cases) than the non-retained cases (45.8% of cases).
Table 2 explains how each of the six variables retained in the model contributed to the final model. The odds ratio represents an association between a particular independent variable and a particular outcome, or for this study, the extent that the independent variables predict membership in the retained outcome group. With categorical variables, this odds ratio represents the likelihood that being in a category increases the odds of being in the retained group over the reference category (i.e., African American/Black participants were 1.779 times more likely to be in the retained group than White/Caucasian students, who served as the reference category). With continuous variables, odds ratios represent the likelihood that quantifiable changes in the independent variables predict membership in the retained group (i.e., for every unit increase in SAT math score, the odds of being in the retained group increase 1.004 times). The interpretation of odds ratios allows them to be viewed as a measure of effect size, with odds ratios closer to 1.0 having a smaller effect (Tabachnick & Fidell, 2013).
Table 2
Variables in the Equation for Hypothesis 1
|
|
|
|
|
95% C.I. for O.R. |
| Variable |
B |
S.E. |
Wald |
O.R. |
Lower |
Upper |
| Ethnicity |
|
|
10.319* |
|
|
|
| Ethnicity (African American/Black) |
.576 |
.393 |
2.148 |
1.779 |
.823 |
3.842 |
| Ethnicity (Hispanic) |
.068 |
.290 |
.054 |
1.070 |
.606 |
1.889 |
| Ethnicity (Asian/Pacific Islander) |
1.889 |
.637 |
8.803** |
6.615 |
1.899 |
23.041 |
| Ethnicity (Other) |
.258 |
.714 |
.131 |
1.295 |
.320 |
5.246 |
| Initial Major |
|
|
35.824*** |
|
|
|
| Initial Major (Declared STEM) |
.412 |
.265 |
2.422 |
1.511 |
.899 |
2.539 |
| Initial Major (Declared Non-STEM) |
-1.944 |
.375 |
26.905*** |
.143 |
.069 |
.298 |
| STEM Seminar (Non-CP) |
.850 |
.258 |
10.885** |
2.340 |
1.412 |
3.879 |
| SAT Math |
.004 |
.002 |
2.411 |
1.004 |
.999 |
1.008 |
| Math Placement–Algebra |
.002 |
.002 |
2.080 |
1.002 |
.999 |
1.005 |
| CTI Total Change |
.017 |
.007 |
5.546* |
1.017 |
1.003 |
1.032 |
| Constant |
-2.994 |
1.378 |
4.717 |
.050 |
|
|
Note: B = Coefficient for the Constant; S.E. = Standard Error; O.R. = Odds Ratio; * p < .05; ** p < .01; *** p < .001.
With logistic regression, the Wald Chi-square test allows the researcher to determine a coefficient’s significance to the model (Tabachnick & Fidell, 2013). Based on this test, Initial Major was the most significant predictor to the model (p < .001). Students in the initially Declared STEM category were 1.511 times more likely to be in the retained group than those in the initially Undeclared category (the reference category); the odds of being in the retained group decreased by a factor of .143 for students in the initially Declared Non-STEM group. The STEM course was the predictor with the second most statistical significance (p < .01), with students in the STEM seminar class being 2.340 times more likely to be in the retained outcome than those in the career planning class. The CTI Total Change score was statistically significant (p < .05), indicating that for every unit increase in CTI Total Change score (i.e., the larger the decrease in score from pretest to posttest), the odds of being in the retained group increase by a factor of 1.017. Ethnicity was a statistically significant predictor (p < .05), with each subcategory having higher odds of being in the retained group than the White/Caucasian group; however, the researchers caution the reader to read these odds ratios for ethnicity with caution because of the number of cases in some categories. SAT Math and Math Placement–Algebra were not statistically significant, but still fell within the recommended inclusion range (p < .20).
Hypothesis 2
Hypothesis 2 stated that the independent variables could predict undergraduate STEM retention from Year 1 to Year 3. As stated previously, the backward stepwise Wald approach involved including all predictors initially and then removing predictors one by one based on p value until all remaining predictors fell within the p ≤ .20 range. This process took six steps, resulting in the removal of five variables with p values greater than .20: (a) CTI Commitment Anxiety Change, (b) CTI Decision Making Confusion Change, (c) Gender, (d) CTI External Conflict Change, and (e) CTI Total Change, respectively. The model yielded a Chi-square value of 55.835 (df = 9, p < .001), a -2 Log likelihood of 307.904, a Cox and Snell R-square value of .191, and a Nagelkerke R-square value of .255. These R-square values indicate that the model can explain between approximately 19% and 26% of the variance in the outcome. The model had a good fit with the data, as evidenced by the Hosmer and Lemeshow Goodness of Fit Test (Chi-square = 9.187, df = 8, p = .327). The model accurately predicted 70.0% of cases across groups. In this analysis, the model predicted the non-retained students more accurately (72.7% of cases) than the retained cases (66.9% of cases).
Table 3 explains how the variables within the model contributed to the final model. Based on the Wald test, Initial Major was the most significant predictor to the model (p < .001). Students in the initially Declared STEM category were 1.25 times more likely to be in the retained group than those in the initially Undeclared category (the reference category); the odds of being in the retained group decreased by a factor of .167 for students in the initially Declared Non-STEM group. The Math Placement–Algebra variable was statistically significant (p < .05), and the odds ratios indicated that for every unit increase in Math Placement–Algebra test score, the odds of being in the retained group are 1.005 higher. The STEM course variable was slightly outside the statistically significant range but fell within the inclusion range, with students in the STEM seminar class being 2.340 times more likely to be in the retained outcome than students in the career planning class. SAT Math was not statistically significant but still fell within the recommended inclusion range (p < .20). Ethnicity also was not a statistically significant predictor but fell within the inclusion range, with each subcategory having higher odds of being in the retained group than the White/Caucasian group; however, the researchers caution the reader to read these odds ratios for ethnicity with caution because of the number of cases in some categories.
Table 3
Variables in the Equation for Hypothesis 2
|
|
|
|
|
95% C.I. for O.R. |
| Variable |
B |
S.E. |
Wald |
O.R. |
Lower |
Upper |
| Ethnicity |
|
|
6.445 |
|
|
|
| Ethnicity (African American/Black) |
.542 |
.448 |
1.467 |
1.719 |
.715 |
4.134 |
| Ethnicity (Hispanic) |
.243 |
.349 |
.484 |
1.275 |
.643 |
2.528 |
| Ethnicity (Asian/Pacific Islander) |
1.636 |
.698 |
5.494* |
5.137 |
1.307 |
20.185 |
| Ethnicity (Other) |
.403 |
.684 |
.347 |
1.497 |
.391 |
5.725 |
| Initial Major |
|
|
17.362** |
|
|
|
| Initial Major (Declared STEM) |
.223 |
.328 |
.460 |
1.250 |
.656 |
2.379 |
| Initial Major (Declared non-STEM) |
-1.792 |
.468 |
14.664** |
.167 |
.067 |
.417 |
| STEM Seminar (Non-CP) |
.588 |
.323 |
3.327 |
1.801 |
.957 |
3.389 |
| SAT Math |
.004 |
.003 |
2.536 |
1.004 |
.999 |
1.010 |
| Math Placement–Algebra |
.005 |
.002 |
5.449* |
1.005 |
1.001 |
1.009 |
| Constant |
-2.994 |
1.378 |
4.717 |
.050 |
|
|
Note: B = Coefficient for the Constant; S.E. = Standard Error; O.R. = Odds Ratio; * p < .05; *** p < .001.
Discussion
The researchers sought to determine the degree to which a set of demographic variables, math scores, and career-related factors could predict undergraduate retention in STEM majors. Based on descriptive statistics, the participants are remaining in STEM majors at a higher rate than other nationwide samples (Chen & Soldner, 2013; Koenig, Schen, Edwards, & Bao, 2012). The sample
in this study was quite different based on gender than what is commonly cited in the literature; approximately 46% of the study’s sample was female, whereas the NCSES (2017) reported that white females made up approximately 31% of those in STEM fields, with minority females lagging significantly behind. The present study’s sample was more in line with national statistics with regard to ethnicity (NCSES, 2017; Palmer et al., 2011).
With Hypothesis 1, the researchers sought to improve on a pilot study (Belser et al., 2017) that did not include demographics or math-related variables. Adding these additional variables did improve the overall model fit and the accuracy of predicting non-retained students, but slightly decreased the accuracy of predicting retained students, as compared to the Belser et al. (2017) model. In addition to improving the model fit, adding in additional variables reversed the claim by Belser et al. (2017) that students in the STEM-focused career planning class were more likely to be retained than the STEM seminar students. In the present study, the STEM seminar students, who declared STEM majors prior to the first day of college, were more likely to be retained in STEM majors, which is in line with prior research connecting intended persistence in a STEM major to observed retention (Le et al., 2014; Lent et al., 2016).
With Hypothesis 2, the researchers sought to expand on the Belser et al. (2017) study by also predicting retention one year farther, into the third year of college. In this endeavor, the analysis yielded a model that still fit the data well. However, this model was much more accurate in predicting the non-retained students and was slightly less accurate in predicting the retained students, with the overall percentage of correct predictions similar to Hypothesis 1. This finding indicates that the included predictors may provide a more balanced ability to predict long-term retention in STEM majors than in just the first year. The initial major and STEM course variables performed similarly as in Hypothesis 1, and as such, similarly to prior research (Le et al., 2014; Lent et al., 2016).
Although sampling issues warrant the reader to read ethnicity results with caution, ethnicity did show to be a good predictor of retention in STEM majors with both Hypotheses 1 and 2. More noteworthy, the African American/Black and Hispanic students had higher odds of being retained. This is inconsistent with most research that shows underrepresented minorities as less likely to be retained in STEM majors (Chen & Soldner, 2013; Cundiff et al., 2013; Gayles & Ampaw, 2014); however, at least one study has previously found results in which ethnic minority students were more likely to be retained in STEM majors (Riegle-Crumb & King, 2010).
Gender was removed as a predictor from both models because of its statistical non-significance. Prior research has shown that females are less likely to be retained in STEM majors (Cundiff et al., 2013; Gayles & Ampaw, 2014; Riegle-Crumb et al., 2012), which separates this sample from prior studies. However, the COMPASS sample did have a larger representation of females than typically observed. Moreover, the COMPASS Program has been mindful of prior research related to gender and took steps to address gender concerns in program development (Dagley et al., 2016).
The continuous variables retained in the models showed only a mild effect on predicting STEM retention. The SAT Math and Math Placement–Algebra scores did perform consistently with prior research, in which higher math scores related to higher odds of retention (CollegeBoard, 2012; Crisp et al., 2009; Le et al., 2014; Mattern & Patterson, 2013; Rohr, 2012). The CTI variables that were retained in the models performed in line with the Belser et al. (2017) pilot study specific to STEM majors and with prior research examining negative career thoughts in undergraduate retention in other majors (Folsom, Peterson, Reardon, & Mann, 2005; Reardon et al., 2015).
Limitations and Implications
The present study has limitations, particularly with regard to research design, sampling, and instrumentation. First, the researchers used a comparison group design rather than a control group, and as such, there were certain observable differences between the two groups. Not having a control group limits the researchers’ ability to make causal claims regarding the predictor variables or the STEM career intervention. The researchers also only included a limited number of predictors; the inclusion of additional variables may have strengthened the models. Although the sample size was sufficient based on the a priori power analysis, the low number of participants in some of the categories may have resulted in overfitting or underfitting within the models. Finally, the researchers were not able to test psychometric properties of the SAT Math subtest or the Math Placement–Algebra subtest with this sample because of not having access to the participants’ item responses for each. The researchers attempted to mitigate limitations as much as possible and acknowledge that they can and should be improved upon in future research.
Future research in this area would benefit from the inclusion of a wider variety of predictor variables, such as math and science self-efficacy, outcome expectations, and internal processes observed with gender and ethnic minority groups (e.g., stereotype threat; Cundiff et al., 2013; Litzler et al., 2014). The researchers also recommend obtaining a larger representation of ethnic minority groups to ensure an adequate number of cases to effectively run the statistical procedure. Future researchers should consider more complex statistical procedures (e.g., structural equation modeling) and research designs (e.g., randomized control trials) to determine more causal relationships between predictors and the outcome variables.
Because the results of this study indicate that a more solidified major selection is associated with higher odds of retention in STEM majors, university career professionals and higher education professionals should strive to develop programming that helps students decide on a major earlier in their undergraduate careers. Structured career development work, often overlooked in undergraduate STEM programming, may be one such appropriate strategy. Additionally, any undergraduate STEM programming must be sensitive to demographic underrepresentation in STEM majors and the STEM workforce and should take steps to provide support for students in these underrepresented groups.
Similar to work with undergraduates, this study’s results provide a rationale for school counselors to engage students in STEM career work so that they can move toward a solidified STEM major prior to enrolling in college. The industry-specific career development work discussed within this study is just as important, if not more important, for students in K–12 settings. Moreover, school counselors, through their continued access to students, can serve as an access point for researchers to learn more about the STEM career development process at an earlier stage of the STEM pipeline. All of these endeavors point to the need for counselor educators to better prepare school counselors, college counselors, and career counselors to do work specifically with STEM and to become more involved in STEM career research.
In the present study, the researchers built upon prior research in the area of STEM retention to determine which variables can act as predictors of undergraduate STEM retention. The binary logistic regression procedure yielded two models that provide insight on how these variables operate individually and within the larger model. Finally, the researchers identified some key implications for counselors practicing in various settings and for researchers who are interested in answering some of the key questions that still exist with regard to STEM career development and retention.
Conflict of Interest and Funding Disclosure
Data collected in this study was part of a dissertation study by the first author. The dissertation was awarded the 2018 Dissertation Excellence Award by the National Board for Certified Counselors.
References
ACT. (2018). The condition of STEM 2017. Retrieved from www.act.org/stemcondition
Agresti, A. (2013). Categorical data analysis (3rd ed.). Hoboken, NJ: Wiley.
Beasley, M. A., & Fischer, M. J. (2012). Why they leave: The impact of stereotype threat on the attrition of women and minorities from science, math, and engineering majors. Social Psychology of Education, 15, 427–448. doi:10.1007/s11218-012-9185-3
Belser, C. T., Prescod, D. J., Daire, A. P., Dagley, M. A., & Young, C. Y. (2017). Predicting undergraduate student retention in STEM majors based on career development factors. The Career Development Quarterly, 65, 88–93. doi:10.1002/cdq.12082
Belser, C. T., Prescod, D. J., Daire, A. P., Dagley, M. A., & Young, C. Y. (2018). The influence of career planning on career thoughts in STEM-interested undergraduates. The Career Development Quarterly, 66(2), 176–181. doi:10.1002/cdq.12131
Bouwma-Gearhart, J., Perry, K. H., & Presley, J. B. (2014). Improving postsecondary STEM education: Strategies for successful interdisciplinary collaborations and brokering engagement with education research and theory. Journal of College Science Teaching, 44, 40–47.
Campbell, D. T., & Stanley, J. C. (1963). Experimental and quasi-experimental designs for research. Chicago, IL: Rand McNally.
Carnevale, A. P., Smith, N., & Melton, M. (2011). STEM: Science, technology, engineering, mathematics. Washington, DC: Georgetown University.
Chen, X., & Soldner, M. (2013). STEM attrition: College students’ paths into and out of STEM fields. Retrieved from http://nces.ed.gov/pubs2014/2014001rev.pdf
Cohen, J. (1992). A power primer. Psychological Bulletin, 112, 155–159. doi:10.1037/0033-2909.112.1.155
CollegeBoard. (2018). Math Test. Retrieved from https://collegereadiness.collegeboard.org/sat/inside-the-test/math
Crisp, G., Nora, A., & Taggart, A. (2009). Student characteristics, pre-college, college, and environmental factors as predictors of majoring in and earning a STEM degree: An analysis of students attending a Hispanic serving institution. American Educational Research Journal, 46, 924–942. doi:10.3102/0002831209349460
Cundiff, J. L., Vescio, T. K., Loken, E., & Lo, L. (2013). Do gender-science stereotypes predict science identification and science career aspirations among undergraduate science majors? Social Psychology of Education, 16, 541–554. doi:10.1007/s11218-013-9232-8
Dagley, M. A., Young, C. Y., Georgiopoulos, M., Daire, A. P., Parkinson, C., Prescod, D. J., & Belser, C. T. (2016). Recruiting undecided admits to pursue a STEM degree. Proceedings from the American Society for Engineering Education 123rd Annual Conference & Exposition. Retrieved from https://peer.asee.org/recruiting-undecided-admits-to-pursue-a-stem-degree
Dempster, A., Laird, N., & Rubin, D. (1977). Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society, Series B, 39, 1–38.
Dixon-Román, E. J., Everson, H. T., & McArdle, J. J. (2013). Race, poverty, and SAT scores: Modeling the influences of family income on black and white high school students’ SAT performance. Teachers College Record, 115, 1–33.
Doerschuk, P., Bahrim, C., Daniel, J., Kruger, J., Mann, J., & Martin, C. (2016). Closing the gaps and filling the STEM pipeline: A multidisciplinary approach. Journal of Science Education and Technology, 25, 682–695. doi:10.1007/s10956-016-9622-8
Ewing, M., Huff, K., Andrews, M., & King, K. (2005). Assessing the reliability of skills measured by the SAT (Report No. RN-24). New York, NY: CollegeBoard. Retrieved from https://files.eric.ed.gov/fulltext/ED562595.pdf
Faul, F., Erdfelder, E., Lang, A. G., & Buchner, A. (2007). G*Power 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behavior Research Methods, 39, 175–191.
Field, A. (2009). Discovering statistics using SPSS (3rd ed.). London, England: Sage Publications.
Folsom, B., Peterson, G. W., Reardon, R. C., & Mann, B. A. (2005). Impact of a career planning course on academic performance and graduation rate. Journal of College Student Retention: Research, Theory & Practice, 6, 461–473. doi:10.2190/4WJ2-CJL1-V9DP-HBMF
Foltz, L. G., Gannon, S., & Kirschmann, S. L. (2014). Factors that contribute to the persistence of minority students in STEM fields. Planning for Higher Education Journal, 42(4), 46–58.
Gall, M. D., Gall, J. P., & Borg, W. R. (2007). Educational research: An introduction (8th ed.). Boston, MA: Allyn & Bacon.
Gayles, J. G., & Ampaw, F. (2014). The impact of college experiences on degree completion in STEM fields at four-year institutions: Does gender matter? The Journal of Higher Education, 85, 439–468.
doi:10.1353/jhe.2014.0022
Gottfredson, L. (1981). Circumscription and compromise: A developmental theory of occupational aspirations. Journal of Counseling Psychology, 28, 545–579. doi:10.1037/0022-0167.28.6.545
Holland, J. L. (1973). Making vocational choices: A theory of vocational personalities and work environments (2nd ed.). Upper Saddle River, NJ: Prentice Hall.
Hosmer, D. W., Jr., Lemeshow, S., & Sturdivant, R. X. (2013). Applied logistic regression (3rd ed.). Hoboken, NJ: Wiley.
Koenig, K., Schen, M., Edwards, M., & Bao, L. (2012). Addressing STEM retention through a scientific thought and methods course. Journal of College Science Teaching, 41(4), 23–29.
Lawlor, S., Richman, S., & Richman, C. L. (1997). The validity of using the SAT as a criterion for black and white students’ admission to college. College Student Journal, 31, 507–515.
Le, H., Robbins, S. B., & Westrick, P. (2014). Predicting student enrollment and persistence in college STEM fields using an expanded P-E fit framework: A large-scale multilevel study. Journal of Applied Psychology, 99, 915–947. doi:10.1037/a0035998
Lent, R. W., Brown, S. D., & Hackett, G. (2002). Social cognitive career theory. In D. Brown (Ed.), Career choice and development (4th ed., pp. 255–311). San Francisco, CA: Jossey-Bass.
Lent, R. W., Miller, M. J., Smith, P. E., Watford, B. A., Lim, R. H., & Hui, K. (2016). Social cognitive predictors of academic persistence and performance in engineering: Applicability across gender and race/ethnicity. Journal of Vocational Behavior, 94, 79–88. doi:10.1016/j.jvb.2016.02.012
Little, R. J. A. (1988). A test of missing completely at random for multivariate data with missing values. Journal of the American Statistical Association, 83, 1198–1202. doi:10.2307/2290157
Little, R. J. A., & Rubin, D. B. (2002). Statistical analysis with missing data (2nd ed.). New York, NY: Wiley.
Litzler, E., Samuelson, C. C., & Lorah, J. A. (2014). Breaking it down: Engineering student STEM confidence at the intersection of race/ethnicity and gender. Research in Higher Education, 55, 810–832.
doi:10.1007/s11162-014-9333-z
Mansfield, K. C., Welton, A. D., & Grogan, M. (2014). “Truth or consequences”: A feminist critical policy analysis of the STEM crisis. International Journal of Qualitative Studies in Education, 27, 1155–1182.
doi:10.1080/09518398.2014.916006
Mattern, K. D., & Patterson, B. F. (2013). The relationship between SAT scores and retention to the second year: Replication with the 2010 SAT validity sample (College Board Statistical Report No. 2013-1). New York, NY: The College Board. Retrieved from https://files.eric.ed.gov/fulltext/ED563087.pdf
National Career Development Association. (2015). Career development theory and its application. Broken Arrow, OK: Author.
National Center for Science and Engineering Statistics. (2017). Women, minorities, and persons with disabilities in science and engineering. Retrieved from https://www.nsf.gov/statistics/2017/nsf17310/
National Science Board. (2018). Science & engineering indicators 2018. Retrieved from https://www.nsf.gov/statistics/2018/nsb20181/
Nosek, B. A., & Smyth, F. L. (2011). Implicit social cognitions predict sex differences in math engagement and achievement. American Educational Research Journal, 48, 1125–1156. doi:10.3102/0002831211410683
Osborn, D. S., Howard, D. K., & Leierer, S. (2007). The effect of a career development course on the dysfunctional career thoughts of racially and ethnically diverse college freshmen. The Career Development Quarterly, 55, 365–377. doi:10.1002/j.2161-0045.2007.tb00091.x
Palmer, R. T., Maramba, D. C., & Dancy, T. E., II (2011). A qualitative investigation of factors promoting the retention and persistence of students of color in STEM. The Journal of Negro Education, 80, 491–504.
Peterson, G. W., Sampson, J. P., Jr., Lenz, J. G., & Reardon, R. C. (2002). A cognitive information processing approach to career problem solving and decision making. In D. Brown (Ed.), Career choice and development (4th ed., pp. 312–369). San Francisco, CA: Jossey-Bass.
Peduzzi, P., Concato, J., Kemper, E., Holford, T. R., & Feinstein, A. R. (1996). A simulation study of the number of events per variable in logistic regression analysis. Journal of Clinical Epidemiology, 49, 1373–1379. doi:10.1016/S0895-4356(96)00236-3
Prescod, D. J., Daire, A. P., Young, C. Y., Dagley, M. A., & Georgiopoulos, M. (in press). Exploring negative career thoughts between STEM declared and STEM interested students. Journal of Employment Counseling, 55(4), 166–176.
Reardon, R., & Fiore, E. (2014). College career courses and learner outputs and outcomes, 1976-2014 (Technical report No. 55). Tallahassee, FL: Center for the Study of Technology in Counseling & Career Development, Florida State University. Retrieved from http://career.fsu.edu/content/download/223105/1906289/TechRept_55_201406.pdf
Reardon, R. C., Melvin, B., McClain, M. C., Peterson, G. W., & Bowman, W. J. (2015). The career course as a factor in college graduation. Journal of College Student Retention: Research, Theory, & Practice, 17, 336–350. doi:10.1177/1521025115575913
Riegle-Crumb, C., & King, B. (2010). Questioning a white male advantage in STEM: Examining disparities
in college major by gender and race/ethnicity. Educational Researcher, 39, 656–664. doi:10.3102/0013189X10391657
Riegle-Crumb, C., King, B., Grodsky, E., & Muller, C. (2012). The more things change, the more they stay the same? Prior achievement fails to explain gender inequality in entry into STEM college majors over time. American Educational Research Journal, 49, 1048–1073. doi:10.3102/0002831211435229
Rohr, S. L. (2012). How well does the SAT and GPA predict the retention of science, technology, engineering, mathematics, and business students? Journal of College Student Retention: Research, Theory, & Practice, 14, 195–208. doi:10.2190/CS.14.2.c
Sampson, J. P., Jr., Peterson, G. W., Lenz, J. G., Reardon, R. C., & Saunders, D. E. (1996a). Career Thoughts Inventory: Professional manual. Odessa, FL: Psychological Assessment Resources.
Sampson, J. P., Jr., Peterson, G. W., Lenz, J. G., Reardon, R. C., & Saunders, D. E. (1996b). Improving your career thoughts: A workbook for the Career Thoughts Inventory. Odessa, FL: Psychological Assessment Resources.
Saunders, D. E., Peterson, G. W., Sampson, J. P., Jr., & Reardon, R. C. (2000). Relation of depression and dysfunctional career thinking to career indecision. Journal of Vocational Behavior, 56, 288–298. doi:10.1006/jvbe.1999.1715
Schneider, K. R., Bickel, A., & Morrison-Shetlar, A. (2015). Planning and implementing a comprehensive student-centered research program for first-year STEM undergraduates. Journal of College Science Teaching, 44(3), 37–43.
Sithole, A., Chiyaka, E. T., McCarthy, P., Mupinga, D. M., Bucklein, B. K., & Kibirige, J. (2017). Student attraction, persistence and retention in STEM programs: Successes and continuing challenges. Higher Education Studies, 7, 46–59. doi:10.5539/hes.v7n1p46
Tabachnick, B. G., & Fidell, L. S. (2013). Using multivariate statistics (6th ed.). Upper Saddle River, NJ: Pearson Education.
Toldson, I. A., & McGee, T. (2014). What the ACT and SAT mean for black students’ higher education prospects. The Journal of Negro Education, 83, 1–3.
Vittinghoff, E., & McCulloch, C. E. (2006). Relaxing the rule of ten events per variable in logistic and Cox regression. American Journal of Epidemiology, 165, 710–718.
Wyatt, J. N., Remigio, M., & Camara, W. J. (2012). SAT Subject Area Readiness Indicators: Reading, Writing, & STEM. Retrieved from https://files.eric.ed.gov/fulltext/ED562872.pdf
Christopher T. Belser, NCC, is an assistant professor at the University of New Orleans. M. Ann Shillingford is an associate professor at the University of Central Florida. Andrew P. Daire is a dean at Virginia Commonwealth University. Diandra J. Prescod is an assistant professor at Pennsylvania State University. Melissa A. Dagley is an executive director at the University of Central Florida. Correspondence can be addressed to Christopher Belser, 2000 Lakeshore Drive, Bicentennial Education Center Room 174, New Orleans, LA 70148, ctbelser@uno.edu.





